
- •1.Комплексные числа. Алгебраическая и тригонометрическая формы, формулы Муавра.
- •2.Матрицы. Линейные операции над ними. Умножение матриц.
- •3.Определители. Свойства определителей.
- •4.Обратная матрица. Решение систем линейных уравнений с помощью обратной матрицы.
- •Свойства обратной матрицы
- •5. Понятие линейной зависимости и независимости строк матрицы. Элементарные преобразования матрицы. Ранг матрицы.
- •7. Теорема Кронекера-Капелли. Решение систем неоднородных линейных уравнений.
- •Следствия
- •8.Теорема Кронекера-Капелли. Однородная система линейных алгебраических уравнений.
- •Следствия
- •9.Понятие вектора. Линейные операции над векторами . Понятие базиса. Координаты вектора. Проекция вектора на ось.
- •1.Сложение векторов.
- •Обозначения
- •10.Линейные комбинации 2, 3, 4-х векторов. Линейная зависимость и независимость векторов.
- •11.Скалярное произведение векторов. Свойства и выражение в декартовых координатах.
- •3.Вычисление проекции вектора на направление другого вектора.(выразить проекцию из
- •12.Векторное произведения векторов. Свойства и выражение в декартовых координатах.
- •13.Смешанное произведение векторов. Свойства и выражение в декартовых координатах.
7. Теорема Кронекера-Капелли. Решение систем неоднородных линейных уравнений.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
Следствия
Количество главных переменных системы равно рангу системы.
Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
Решение систем неоднородных линейных уравнений.
Неоднородной системой
линейных уравнений называется
система вида:
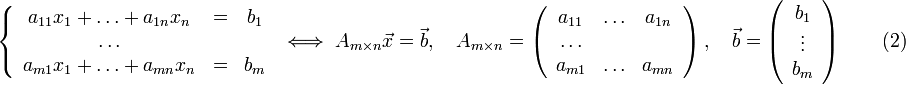
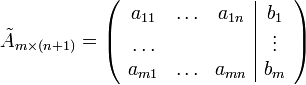 —
её
расширенная матрица.
—
её
расширенная матрица.
Теорема
(об общем решении неоднородных
систем).
Пусть
![]() (т.е.
система (2) совместна), тогда:
(т.е.
система (2) совместна), тогда:
если
 ,
где
,
где 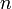 —
число переменных системы (2), то решение
(2) существует и оно единственно;
—
число переменных системы (2), то решение
(2) существует и оно единственно;если
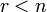 ,
то общее решение системы (2) имеет вид
,
то общее решение системы (2) имеет вид  ,
где
,
где 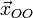 —
общее решение системы (1), называемое общим
однородным решением,
—
общее решение системы (1), называемое общим
однородным решением, 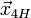 —
частное решение системы (2), называемое частным
неоднородным решением.
—
частное решение системы (2), называемое частным
неоднородным решением.
Пример
Решим систему
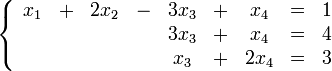
Преобразуем
её к

Тогда
переменные ![]() и
и ![]() обязательно
будут главными, возьмём также
обязательно
будут главными, возьмём также ![]() в
качестве главной.
в
качестве главной.
Заметим,
что ![]() является
частным решением.
является
частным решением.
Составим
однородную систему:
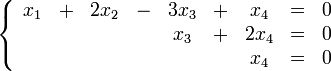
Тогда,
подставив единицу в качестве свободной
переменной ![]() ,
получим ФСР однородной системы:
,
получим ФСР однородной системы:
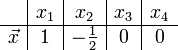
Общее решение системы может быть записано так:
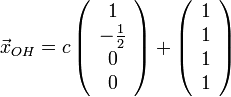
8.Теорема Кронекера-Капелли. Однородная система линейных алгебраических уравнений.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
Следствия
Количество главных переменных системы равно рангу системы.
Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
Однородная система линейных алгебраических уравнений.
Однородной
системой линейных уравнений называется
система вида:
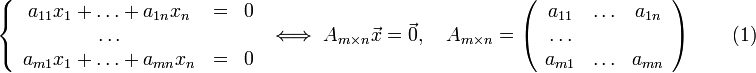
Нулевое
решение ![]() системы
(1) называется тривиальным
решением.
системы
(1) называется тривиальным
решением.
Однородные системы всегда совместны, т.к. всегда существует тривиальное(единственное) решение.
Если существует любое ненулевое решение системы, то оно называется нетривиальным.
Пример
Решим систему
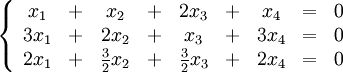
Перепишем её в матричном виде:
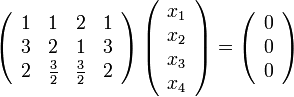
Путём элементарных преобразований над строками приведём её основную матрицу к ступенчатому виду:
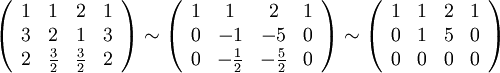
Таким
образом ранг системы
(ранг её основной матрицы) равен двум.
Это значит, что существует ![]() линейно
независимых решения
системы.
линейно
независимых решения
системы.
Перепишем полученную систему в виде уравнений:

Возьмём и в качестве главных переменных. Тогда:
![]()
Подставим
по очереди единицы в качестве одной из
свободных переменных: ![]() и
и ![]() .
.
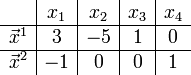
Тогда общее решение рассматриваемой системы может быть записано так:
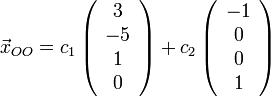 ,
,
а
вектора 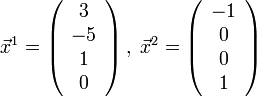 составляют
фундаментальную систему решений.
составляют
фундаментальную систему решений.
