1.Комплексные числа. Алгебраическая и тригонометрическая формы, формулы Муавра.
Множество комплексных чисел – объединения множеств действительных и мнимых чисел.
Элементы этого множества записываются в виде: Z=X+iY, где X,Y –действительные числа, X-действительная часть, Y-мнимая часть. i – мнимая единица.
-
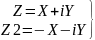сопряженные комплексные числа.
-
противоположные комплексные числа.
Действия над К.Ч: сложение, вычитание, деление, умножение.
Степени
числа i
:
;
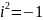; i
в 1 степени равно
.
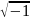Z=X+iY |
|
X=
r*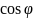
,
Y=
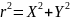r*
,
, r
=
- формулы переходы от алгебраической
к тригонометрической форме К.Ч.
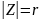
Z=X+iY
Z=r*
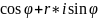
Z=
r * ( |
)Нахождение Аргумента К.Ч.
=
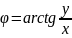
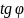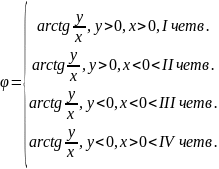
Формулы Муавра:
*(
),
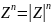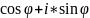
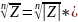k=0,1,…,n-1,
n
корней расположенных в вершинах
правильного n-угольника
вписанного в окружность с центром в
начале координат и R=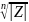
.
2.Матрицы. Линейные операции над ними. Умножение матриц.
Матрицы размера MxN, где M-число строк, а N-число строк, называется таблица чисел расположенных в определенном порядке. Эти числа называются элементами матрицы.
Если M=N,то матрица называется квадратной. Матрица, у которой по главной диагонали все элементы единицы ,а остальные элементы нули, называется единичной матрицей( матрица «E»).
Линейные операции над ними.
Сложение(вычитание) матриц.
Замечание: Сложение(вычитание) матриц определено только для матриц одного размера.
Результатом сложения(вычитания) матриц- является матрица элементами, которой будут соответственно сложение(вычитание) элементов исходных матриц.
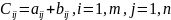A+B=C
1.A+B=B+A(коммуникативность).
2.(A+B)+C=A+(B+C).(сочетательный(ассоциативность).
Умножение(деление) матриц на число- это умножение(деление) матрицы на это число.
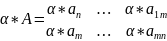
3.
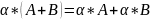(Дистрибутивность).
4.(α+β)*A=α*A+β*A.
Умножение матриц.
Операция умножение матриц определена только если число столбцов первой матрицы равно числу строк второй матрицы.
Опр: Умножение 2-х матриц A и B называется матрица C элементы которой определяются из формулы:
|
3.Определители. Свойства определителей.
Определитель- это число. (разность произведений главной диагонали и побочной.(в матрице 2х2;а в остальных ты тоже знаешь как находить определитель)).
Правило Минора:
Минором
любого элемента
матрицы N-го
порядка называется определитель порядка
n-1,
соответствующей матрицы полученной из
исходной вычеркиванием i
строки
и
j
столбца.
Теорема:
Каков бы ни был № строки i для определителя n-го порядка справедлива формула:
-
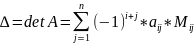формула разложения по i
строке.
это
сумма произведений элементов любой
строки(или столбца) на их алгебраические
дополнения.
Свойства определителей:
1.Величина определителей не изменяется, если поменять местами столбцы и строки.
2.Перестановка 2-х строк(столбцов) равносильно его умножению на (-1).
3. Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.
4.Общий множитель всех элементов строки(столбца) можно выносить за знак определителя.
5.Если 2-е (или несколько) строк(столбцов) пропорциональны, то определитель =0
6.Сумма произведений элементов какой-либо строки на алгебраическое дополнение соответствующих элементов другой строки равна 0.
7.Определитель произведения = произведению определителей.
При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.
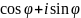