- •1.Основные физические свойства жидкости.
- •2.Силы, действующие в жидкости.
- •3.Давление в точке покоящейся жидкости.
- •Диф. Уравнение равновесия жидкости.
- •5. Основное уравнение гидростатики.
- •6. Давление жидкости на плоскую стенку. Центр давления.
- •7.Сила давления жидкости на криволинейную стенку. Тело давления.
- •Способы описания движения жидкости.
- •10.Поток. Гидравлические элементы потока.
- •11. Уравнение неразрывности (сплошности) потока.
- •12.Диф. Уравнение движения и баланса энергии для невязкой жидкости.
- •1 3.Уравнение бернулли для элементарной струи невязкой жидкости.
- •14.Уравнение бернулли для элементарной струи и потока вязкой жидкости.
- •15.Уравнение гидравлического количества движения (уравнение импульсов).
- •16.Общие сведения о потерях напора по длине и в местных сопротивлениях. Режимы движения жидкости. Число рейнольдса.
- •17.Режим движения жидкости. Число рейнольдса
- •18.Закон распределения скорости по сечению
- •19.Расход жидкости и средняя скорость потока
- •20.Закон гидравлического сопротивления коэффициента дарси
5. Основное уравнение гидростатики.
В ыделим
вокруг точки А элементарный объем
жидкости
в виде параллелепипеда, точка находится
на глубине h
от свободной поверхности жидкости или
на расстоянии Z
от нижней плоскости выделенного объема,
проекции единичных массовых сил на
координатные оси в данном случае будут
равны
ыделим
вокруг точки А элементарный объем
жидкости
в виде параллелепипеда, точка находится
на глубине h
от свободной поверхности жидкости или
на расстоянии Z
от нижней плоскости выделенного объема,
проекции единичных массовых сил на
координатные оси в данном случае будут
равны
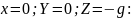
Подставив данные значения в уравнение равновесия жидкости получим:
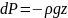
Проинтегрировав
данное выражение, получим
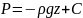 .
Постоянную интегрирования С определим
из следующих начальных условий Z=Z0,
и
p=p0
.
Постоянную интегрирования С определим
из следующих начальных условий Z=Z0,
и
p=p0
Тогда
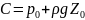 , а выражение для давления запишем в
виде
, а выражение для давления запишем в
виде
 или
или
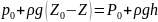
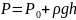
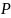 -абсолютное
и полное давление в точке покоящейся
жидкости;
-абсолютное
и полное давление в точке покоящейся
жидкости;
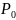 -
абсолютное или полное давление окружающей
среды;
-
абсолютное или полное давление окружающей
среды;
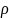 -
плотность жидкости;
-
плотность жидкости;
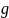 -
ускорение силы тяжести;
-
ускорение силы тяжести;
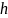 -
глубина погружения точки;
-
глубина погружения точки;
Если
Р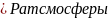 ,
то
,
то
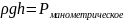 .
Оно показывает на сколько давление в
данной точке жидкости превышает
атмосферное давление (избыточное)
изменяется от 0 до
.
Оно показывает на сколько давление в
данной точке жидкости превышает
атмосферное давление (избыточное)
изменяется от 0 до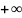
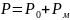
Если
Р
,
то
 . Оно показывает на сколько давление в
данной точке жидкости не достает до
давления атмосферного от 0-Ратмосферного.
. Оно показывает на сколько давление в
данной точке жидкости не достает до
давления атмосферного от 0-Ратмосферного.
6. Давление жидкости на плоскую стенку. Центр давления.
М ысленно
выделим на плоской боковой стенке
сосуда, наклоненного под углом
ысленно
выделим на плоской боковой стенке
сосуда, наклоненного под углом
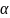 к горизонту, произвольную фигуру
площадью F и определим действующую на
нее со стороны жидкости силу давления
Р. Так как давление жидкости в различных
по высоте точках площади F неодинаково,
выделим на этой площади элементарную
площадку dF,
находящуюся на расстоянии h
от свободной поверхности жидкости.
Ввиду незначительных размеров площадки
будем полагать, что давление по высоте
на нее не изменяется, а во всех ее точках
одинаково и равно
к горизонту, произвольную фигуру
площадью F и определим действующую на
нее со стороны жидкости силу давления
Р. Так как давление жидкости в различных
по высоте точках площади F неодинаково,
выделим на этой площади элементарную
площадку dF,
находящуюся на расстоянии h
от свободной поверхности жидкости.
Ввиду незначительных размеров площадки
будем полагать, что давление по высоте
на нее не изменяется, а во всех ее точках
одинаково и равно
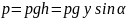 ,
следовательно, сила давления жидкости
на элементарную площадку dF ;
,
следовательно, сила давления жидкости
на элементарную площадку dF ;
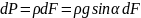
Сила давления на всю рассматриваемую площадку:
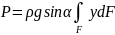
Выражение
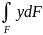 представляет собой статический момент
рассматриваемой площади относительно
оси х, равный произведению площади
этой фигуры F на расстояние от ее центра
тяжести до оси х, т. е. ycF.
Таким образом, Р = ρg sin α ycF
или, учитывая, что yc sinα = hc,
а давление в центре тяжести рс.
представляет собой статический момент
рассматриваемой площади относительно
оси х, равный произведению площади
этой фигуры F на расстояние от ее центра
тяжести до оси х, т. е. ycF.
Таким образом, Р = ρg sin α ycF
или, учитывая, что yc sinα = hc,
а давление в центре тяжести рс.
То:
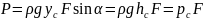
Таким образом сила давления жидкости на плоскую стенку Р равна произведению площади стенки F, смоченной жидкостью, на гидростатическое давление в ее центре тяжести pc = ρghc .
Кроме
численного выражения силы давления
жидкости необходимо определить и
координату её приложения – центр
давления. Предположим что сила давления
Р приложена в точке D,
находиться на расстоянии yd
от оси х. В соответствии с теоремой
Вариньона имеем:
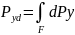 . Подставив значение Р и dP
в
это выражение получим:
. Подставив значение Р и dP
в
это выражение получим:
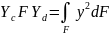
Выражение
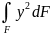 представляет собой момент инерции jx
площади фигуры относительно оси х,
который может быть выражен через момент
инерции j
относительно центральной оси, параллельно
центральной оси х.
представляет собой момент инерции jx
площади фигуры относительно оси х,
который может быть выражен через момент
инерции j
относительно центральной оси, параллельно
центральной оси х.
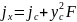
Тогда:
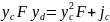
Откуда:
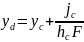
Глубина
погружения центра давления от свободной
поверхности:
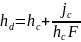
Из последних двух уравнений видно, что центр давления расположен ниже центра тяжести.
В
частном случае когда требуется определить
силу давления жидкости на плоское дно
сосуда используют формулу :