33. Критерий пессимизма-оптимизма Гурвица оптимальности чистых стратегий относительно выигрышей и рисков. Вероятностная интерпретация коэффициентов критерия Гурвица.

Данный критерий позволяет учитывать комбинацию наихудших состояний. Другими словами, при выборе решения мы находим некоторый средний результат при состоянии, находящемся между крайним пессимизмом и безудержным оптимизмом.

Критерий Гурвица целесообразно применять в следующих ситуациях:

1. Информация о состояниях окружающей среды отсутствует или недостоверна;

2. Необходимо считаться возможным появлением наихудшего и наилучшего состояния природы;

3. Допускается некоторый риск.

Рассмотрим игру с природой размера m x n, m 2, n 2, с матрицей A= (a_ij), где i=1,2,…,m, а j=1,2,…,n. Пусть A₁ ,A₂ ,…,A_m – чистые стратегии игрока А и П₁,П₂,...П_n – состояния природы П. Вероятности состояний неизвестны.

Введём специальный коэффициент λ [0,1], которым обозначим количественную «меру оптимизма» игрока А при выборе стратегии. Данный коэффициент выбирает сам игрок, на основании интуиции, личного опыта, состояния окружающей среды или на основе статистических исследований результатов принятия решений.

Эффективность чистой стратегии A_i в смысле критерия Гурвица [(Hur)^p (λ)] характеризуется показателем:

(Hur)^p_i (λ)= (1- λ)W_i + λM_i , i = 1,2,…,m, (2.1)

где W_i и M_i - показатели эффективности стратегии A_i соответственно по критерию Вальда и по максимаксному критерию.

Оптимальной во множестве чистых стратегий по критерию Гурвица с коэффициентом λ относительно выигрышей, или (Hur)^p (λ) – оптимальной во множестве 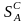, называется чистая стратегия A_k с наибольшим (Hur)^p (λ)-показателем эффективности:

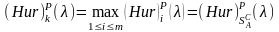
Ценой игры в чистых стратегиях по критерию Гурвица с коэффициентом оптимизма λ относительно выигрышей или (Hur)^p (λ)-ценой в чистых стратегиях называется максимальный из показателей эффективности:

Вероятностная интерпретация коэффициентов критерия Гурвица.

Данный критерий позволяет учитывать комбинацию наихудших состояний. Смысл его состоит в нахождении по специальной формуле эффективности всех стратегий игрока А и последующее сравнении данных показателей эффективности для выбора наиболее оптимальной стратегии, при условии полной неопределённости, т.е. вероятности состояния природы нам неизвестны. Другими словами, при выборе решения мы находим некоторый средний результат при состоянии, находящемся между крайним пессимизмом и безудержным оптимизмом.

Критерий Гурвица целесообразно применять в следующих ситуациях:

1. Информация о состояниях окружающей среды отсутствует или недостоверна;

2. Необходимо считаться возможным появлением наихудшего и наилучшего состояния природы;

3. Допускается некоторый риск.

Рассмотрим игру с природой размера m x n, m 2, n 2, с матрицей A= (a_ij), где i=1,2,…,m, а j=1,2,…,n. Пусть A₁ ,A₂ ,…,A_m – чистые стратегии игрока А и П₁,П₂,...П_n – состояния природы П. Вероятности состояний неизвестны.

Введём специальный коэффициент λ [0,1], которым обозначим количественную «меру оптимизма» игрока А при выборе стратегии. Данный коэффициент выбирает сам игрок, на основании интуиции, личного опыта, состояния окружающей среды или на основе статистических исследований результатов принятия решений.

Эффективность чистой стратегии A_i в смысле критерия Гурвица [(Hur)^p (λ)] характеризуется показателем:

(Hur)^p_i (λ)= (1- λ)W_i + λM_i , i = 1,2,…,m, (2.1)

где W_i и M_i - показатели эффективности стратегии A_i соответственно по критерию Вальда и по максимаксному критерию.

Таким образом, Игрок А при использовании критерия Гурвица с коэффициентом λ [0,1] занимает более взвешенную позицию, чем если бы он применил критерий Вальда или максимаксный критерий.

Если открыть скобки в равенстве (2.1) и несколько преобразовать данное выражение, то можно получить показатель эффективности (Hur)^p_i (λ) в форме линейной функции от аргумента λ [0,1] с угловым коэффициентом (M_i -W_i):

(Hur)^p_i (λ) = (M_i -W_i) λ + W_i (2.2)

Ценой игры в чистых стратегиях по критерию Гурвица с коэффициентом оптимизма λ относительно выигрышей или (Hur)^p (λ)-ценой в чистых стратегиях называется максимальный из показателей эффективности:

(2.3)

Оптимальной во множестве чистых стратегий по критерию Гурвица с коэффициентом λ относительно выигрышей, или (Hur)^p (λ) – оптимальной во множестве , называется чистая стратегия A_k с наибольшим (Hur)^p (λ)-показателем эффективности:

(2.4)

Природа может находиться в самом выгодном положении с вероятностью λ и в самом невыгодном с вероятностью (1- λ). Можно также трактовать параметр λ как степень оптимизма лица, принимающего решения.