27.Критерий Байеса оптимальности чистых стратегий относительно выигрышей.

Иначе называется критерием математического ожидания. Используется для решения задач в условиях риска.

Пусть известны состояния П­₁ … П­_n и вероятности q₁ … q_{n ,} с которыми природа П реализует эти состояния. Тогда мы находимся в ситуации принятия решения в условиях риска. Показателем эффективности стратегии по критерию Байеса относительно выигрышей называется среднее значение, или математическое ожидание выигрыша i-й строки с учётом вероятностей всех возможных состояний природы: , .

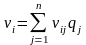Оптимальной среди чистых стратегий по критерию Байеса относительно выигрышей считается стратегия с максимальным показателем эффективности: (матрица выигрышей), 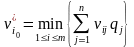(матрица потерь).

Критерий Байеса относительно выигрышей и относительно рисков эквивалентны, т.е. если стратегия S_io является оптимальной по критерию Байеса относительно выигрышей, то она является оптимальной и по критерию Байеса относительно рисков, и наоборот.

Пример.

	,	,	,	vi
S1	2	6	4	4,6
S2	5	1	3	2,4

Для матрицы выигрышей: , .

Для матрицы потерь: ,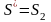

28.Критерий Байеса оптимальности чистых стратегий относительно рисков.

Рассмотрим игру с природой с матрицей, в которой известны вероятности состояния природы q₁ .. q_n. При принятии решения в условиях риска можно пользоваться не только средними выигрышами, но и средними рисками. Составим матрицу рисков для матрицы исходной, использую формулу рисков:

r _i,j =

Показателем неэффективности стратегии S_i по критерию Байеса относительно рисков называется среднее значение (мат ожидание) рисков i-й строки матрицы А, вероятности которых, совпадают с вероятностями природы. Пусть средний риск при стратегии S_i равен

Показателем неэффективности стратегии по критерию Байеса относительно рисков называется среднее значение рисков i-й строки матрицы рисков: .

Соответствующий критерий: .

Тогда оптимальной среди чистых стратегий по критерию Байеса относительно рисков является стратегия S_io, показатель неэффективности которой минимален, т.е. минимален средний риск.

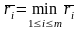
Критерий Байеса относительно выигрышей и относительно рисков эквивалентны, т.е. если стратегия S_io является оптимальной по критерию Байеса относительно выигрышей, то она является оптимальной и по критерию Байеса относительно рисков, и наоборот.

Пример для матрицы выигрышей.

	,	,	,
S1	2	6	4
S2	5	1	3

Из наибольшего числа каждого столбца вычитаем каждое число данного столбца. Стратегия S₁ является оптимальной по критерию Байеса относительно рисков, так как наименьший показатель неэффективности именно у этой стратегии (0,6). ,

	,	,	,
S1	3	0	0	0,6
S2	0	5	1	2,8

29.Критерий Лапласа оптимальности чистых стратегий относительно выигрышей.

Иначе называется – принцип недостаточного основания.

Часто складывается такая ситуация, когда мы лишены возможности определить вероятности состояния природы.

Критерий основан на принципе недостаточного основания. Здесь все вероятности состояний природы признаются равновероятными: . Тогда показателем эффективности стратегии по критерию Лапласа относительно выигрышей называется среднее арифметическое выигрышей i-й строки: .

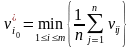Оптимальной среди чистых стратегий по критерию Лапласа относительно выигрышей считается стратегия с максимальным показателем эффективности: (матрица выигрышей), (матрица потерь).

Очевидно, что критерий Лапласа относительно выигрышей есть частный случай критерия Байеса относит выигрышей при .

				vi
S1	2	6	4	4
S2	5	1	3	3

Для матрицы выигрышей: , .

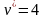Для матрицы потерь: ,
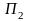
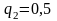