49.Позиционная форма игры.

Одним из классов игр, описывающих конфликты, динамика которых оказывает влияние на поведение участников, являются так называемые позиционные игры.Позиционная игра – это бескоалиционная игра, моделирующая процессы последовательного принятия решений игроками в условиях меняющейся во времени и, вообще говоря, неполной информации.

Процесс самой игры состоит в последовательном переходе от одного состояния игры к другому, который осуществляется либо путём выбора игроками одного из возможных действий в соответствии с правилами игры, либо случайным образом.

В позиционной игре состояния игры принято называть позициями, а возможные выборы в каждой позиции – альтернативами.

Характерной особенностью позиционной игры является возможность представления множества позиций в виде древовидного упорядоченного множества, которое называется деревом игры

Пользуясь графическим описанием игры, можно сказать, что процесс игры состоит в переходе от начальной позиции к окончательной через непосредственно следующие одна за другой промежуточные позиции.

Каждая окончательная вершина определяет единственную цепь (последовательность идущих друг за другом звеньев), связывающую начальную вершину с данной

Такая цепь называется партией. Число различных партий равно числу окончательных вершин.

В каждой окончательной позиции задан числовой выигрыш игроков.

Различают позиционные игры с полной информацией и позиционные игры с неполной информацией. Игры с полной информацией образуют наиболее простой класс позиционных игр.

50.Понятие о конечных позиционных играх с совершенной информацией.

Позиционная игра – это бескоалиционная игра, моделирующая процессы последовательного принятия решений игроками в условиях меняющейся во времени и, вообще говоря, неполной информации.

Различают позиционные игры с полной информацией и позиционные игры с неполной информацией. Игры с полной информацией образуют наиболее простой класс позиционных игр.

Не вполне строго, но практически можно считать, что игра является игрой с полной информацией, если:

• игроки воздействуют на игровую ситуацию дискретными действиями — ходами, порядок ходов определён правилами и не зависит от таких параметров, как скорость реакции игроков (то есть очередной ход делает тот, кто должен его сделать по правилам, а не тот, кто первым догадался или успел его сделать);

• в любой момент игры все игроки имеют полную информацию о состоянии игры, то есть о позиции и всех возможных ходах любого из игроков.

Любая игра называется конечной, если она содержит конечное множество игроков , множества чистых стратегий содержат конечное число элементов (стратегий). Дерево такой игры, записанное в позиционной форме, будет иметь конечное множество вершин.

Позиционные игры также можно разделить на игры с совершенной информацией и несовершенной информацией.

В игре с совершенной информацией каждый игрок всегда знает точно, в каком месте дерева игры он находится, нет одновременных ходов, и все игроки наблюдают ходы природы (если таковые имеются).

Определение 9.2. Игра в позиционной форме называется игрой с совершенной информацией, если каждое информационное множество состоит из единственной вершины (рис. 9.3). В противном случае игра называется игрой с несовершенной информацией.

Определение 9.3. Стратегией в позиционной игре называется полный возможный план действий, который говорит, что игрок будет делать в каждом его информационном множестве.

(антагонистическая игра с совершенной информацией)

1-й ход. Игрок A выбирает число x из множества двух чисел .

2-й ход. Игрок B выбирает число y из множества двух чисел , зная выбор числа x игроком A.

Функция выигрышей игрока A за счёт игрока B задаётся так:

, , , .

На рис. 9.4 показаны дерево игры и информационные множества (оранжевый пунктир).

• 

51.Стратегическая форма позиционной игры с совершенной информацией.

Позиционная игра – это бескоалиционная игра, моделирующая процессы последовательного принятия решений игроками в условиях меняющейся во времени и, вообще говоря, неполной информации.

В игре с совершенной информацией каждый игрок всегда знает точно, в каком месте дерева игры он находится, нет одновременных ходов, и все игроки наблюдают ходы природы (если таковые имеются).

Игра в позиционной форме называется игрой с совершенной информацией, если каждое информационное множество состоит из единственной вершины (см. рисунок)

Пример : (антагонистическая игра с совершенной информацией)

1-й ход. Игрок A выбирает число x из множества двух чисел .

2-й ход. Игрок B выбирает число y из множества двух чисел , зная выбор числа x игроком A.

Функция выигрышей игрока A за счёт игрока B задаётся так:

, , , .

На рис. 9.4 показаны дерево игры и информационные множества (оранжевый пунктир).

Рис. 9.4. Дерево игры с совершенной информацией

52.Равновесие в позиционной игре. Принцип последовательной рационализации.

Теорема:В конечной (позиционной) игре с совершенной информацией существует равновесие по Нэшу в чистых стратегиях. Обсуждение данного факта мы начнём с примера, который покажет, что равновесие по Нэшу не всегда даёт разумное предсказание.

Пример. Фирма E (entrant) – новичок – рассматривает вопрос о том, входить ли на рынок, где в текущий момент есть одна единственная укоренившаяся фирма I (incumbent). Если E решается на вход, то I может ответить двумя способами: она может предоставить вход, отдавая часть своих продаж, но, не изменяя цену, либо она может вступить в хищническую войну, которая приведёт к «драматическому» снижению цен. Дерево данной игры представлено на рис. 9.8.

Рис. 9.8. Дерево игры «Борьба за рынок»

Стратегии игрока E:

– не входить на рынок;

– входить на рынок.

Стратегии игрока I:

– объявить войну игроку E, если он вошёл в рынок;

– предоставить игроку E вход, отдавая часть своих продаж, но, не изменяя цену.

Соответствующая игре нормальная форма имеет вид:

		I
E		(0, 2)	(0, 2)
		(−3, −1)	(2, 1)

В этой игре две равновесных по Нэшу ситуации (0, 2) и (2, 1) в чистых стратегиях. Но первая из этих ситуаций представляет собой предсказание, не являющееся разумным. Для того чтобы исключить ситуации типа мы рассмотрим принцип последовательной рационализации, который составляет основу метода обратной индукции – основного метода решения позиционных игр: оптимальная стратегия игры должна предписывать оптимальный ход в каждой вершине дерева. Т.е., если игрок находится в некоторой вершине дерева, его стратегия должна предписывать оптимальный выбор, начиная с этой точки, при данных стратегиях его оппонентов. Согласно данному принципу стратегия не является оптимальной, поскольку рассматриваемые в игре ответы I имеют смысл, только если фирма E вошла на рынок. Если игрок E вошёл на рынок, оптимальным поведением игрока I будет предоставить возможность E действовать на рынке.

Итак, после того как E выбрал стратегию , оптимальной стратегией для игрока I будет . Теперь мы можем определить оптимальное поведение фирмы E до её входа на рынок. Это можно сделать, рассмотрев редуцированную позиционную форму, где после входа на рынок игрока E принятие решения игроком I заменено на соответствующие выигрыши, которые возникают при оптимальном его поведении (рис. 9.9).

Рис. 9.9. Дерево редуцированной игры «Борьба за рынок»

В результате получаем простейшую задачу индивидуального решения, причём очевидным является решение игрока E войти на рынок.

Обратная индукция и конечные игры с совершенной информацией

Для того чтобы внимательнее посмотреть на обратную индукцию в конечной игре с совершенной информацией, начнём с определения оптимального «действия» в последних вершинах дерева, где принимается решение (т.е. тех вершин, для которых «последователи» – это только терминальные вершины). Решение, принимаемое игроком в такой вершине, не зависит уже от стратегического взаимодействия и потому является простой задачей принятия решения. Затем мы может обратиться к «предпоследней» вершине и найти оптимальное решение там, предвидя, естественно, ход, который будет сделан в последней вершине. И так далее.

Рассмотрим следующий пример позиционной игры (рис. 9.10):

Рис. 9.10. Дерево неантагонистической позиционной игры 3-х игроков

Принимая оптимальные решения для третьего игрока в последних вершинах дерева, приходим к первой редуцированной игре следующего вида (рис. 9.11):

Рис. 9.11. Редуцированная игра после принятия решения третьим игроком

Принимая оптимальное решение для второго игрока, получаем вторую редуцированную игру (рис. 9.12):

Рис. 9.12. Редуцированная игра после принятия решения вторым

игроком

Опишем с учётом наших последовательных рассуждений оптимальные стратегии игроков:

, т.к. ;

, если игрок 1 играет R, т.к. ;

Игровая ситуация является равновесной по Нэшу. Игрок отклонившись в единоличном порядке от своей оптимальной стратегии может лишь ухудшить своё положение. Найденное решение игры проведено в соответствии с принципом последовательной рационализации.

В любой конечной игре с совершенной информацией существует ситуация равновесия по Нэшу в чистых стратегиях, которая может быть найдена с помощью обратной индукции. Более того, если ни один из игроков не имеет одинаковых выигрышей ни в одной из терминальных вершин, то существует единственное равновесие по Нэшу, которое может быть полученное методом обратной индукции.

53.Модель дуополии Штакельберга.

Дуополия по Штакельбергу – это модификация дуополии по Курно. Теперь мы считает, что есть лидер, который делает ход первым. Затем, зная этот выбор, другой игрок делает свой ход.

Итак, игра протекает следующим образом:

1. фирма 1 выбирает ;

2. фирме 2 становится известна величина , и после этого она выбирает ;

3. Выигрыш фирмы определяется формулой , .

Для нахождения равновесия воспользуемся обратной индукцией. Определим сначала функцию реагирования фирмы 2, решая задачу

.

Привлекая необходимое условие существования экстремума получаем функцию реагирования . То же самое было и в случае дуополии Курно. Разница, однако, в том, что действительная, а не гипотетическая функция реагирования фирмы 2.

Фирма 1, естественно, также может вычислить эту функцию реагирования, а, следовательно, задача фирмы 1 выглядит так:

,

что даёт и .

Прибыль в случае дуополии по Штакельбергу:

, .

Для сравнения в модели Курно:

.

54.Модель последовательного торга.

Рассмотрим следующую игру. Игроки 1 и 2 торгуются о разделе 1 доллара: 1-й игрок предлагает некоторый способ деления, 2-й либо принимает это предложение, либо нет; если нет, то он предлагает способ деления, а 1-й принимает, либо нет и т.д.

Каждое предложение занимает один период, но при этом есть дисконтирующий множитель. Итак, формально рассмотрим следующую трёхпериодную (трёхшаговую) игру.

1.а) В начале первого периода игрок 1 предлагает «свою долю» доллара, оставляя игроку 2.

1.b) Игрок 2 принимает предложение, тогда игра заканчивается, либо отклоняет его. В этом случае игра переходит ко 2-му периоду.

2.a) В начале второго периода игрок 2 предлагает долю , которую получает игрок 1, оставляя себе .

2.b) Игрок 1 либо принимает предложение, либо нет. В последнем случае игра переходит к 3-му периоду.

3) Игроки в третьем периоде получают доли , , причём d задан экзогенно.

Решим данную задачу с помощью метода обратной индукции. Сначала вычислим, что происходит, если дело доходит до 2-го периода. Игрок 1 может получить d, если отклонит . С учётом дисконтирования (мы сравниваем стоимость в разных (соседних) периодах) игрок 1 примет тогда и только тогда, когда , – коэффициент дисконтирования. Это значит, что задача игрока 2 состоит в выборе между получением и получением в следующем периоде. Дисконтированная стоимость последнего действия есть , что меньше, чем , а потому игрок 2 во втором периоде предлагает .

Таким образом, если игра доходит до второго периода, то 2-й игрок предложит , и игрок 1 примет это предложение.

Однако игрок 1 может предвидеть, что игрок 2 может получить во втором периоде, отклоняя предложение . В первом периоде стоимость с учётом дисконтирования составит . Значит, игрок 2 принимает тогда и только тогда, когда , или .

Поэтому задача игрока 1 в первом периоде состоит в выборе между получением в этом периоде и получением в следующем периоде. Дисконтированная величина составляет , что меньше, чем . Значит, оптимальное предложение в первом периоде есть . Следовательно, в первом периоде игрок 1 предлагает , а игрок 2 принимает это предложение и получает . Таким образом, выигрыш игроков есть и соответственно.

55.Модель «инвесторы и банк»:

Представим следующую ситуацию. Два инвестора вкладывают по D долларов в банк. Банк инвестировал эти средства в долгосрочный проект. Если форс-мажорные обстоятельства заставляют банк ликвидировать свои инвестиции до того, как проект «созревает», то он покрывает некоторую сумму , где . Если банк позволяет проекту «созреть», то проект принесёт , .

Есть два периода, когда вкладчики могут забрать свой вклад: период 1 – до «созревания», период 2 – после созревания. Для упрощения не будем учитывать дисконтирование. Если оба вкладчика забирают вклады в период 1, то оба получают по r и игра заканчивается. Если только один вкладчик забирает в период 1, то он получает D, а второй получает . Наконец, если ни один вкладчик не забирает в период 1, то проект «созревает», и оба вкладчика забирают свои деньги в период 2, и каждый получает по R. Если только один вкладчик забирает деньги в период 2, то он получает , другой получает D. Если, наконец, ни один не забирает в период 2, то банк возвращает по R каждому.

Дерево игры изображено на рис. 8.16.

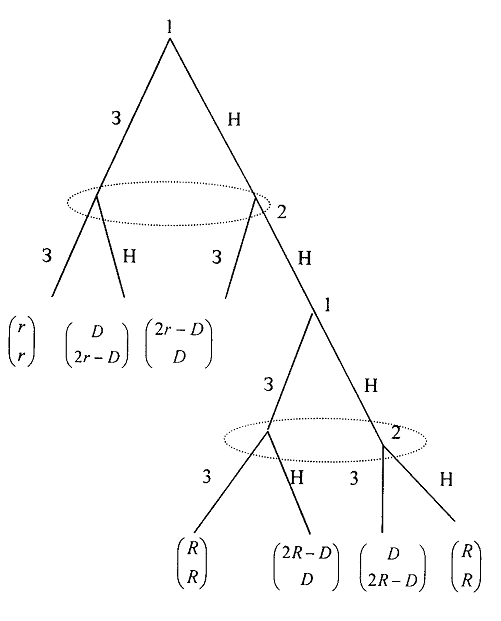
Рис. 8.16.

Без строгой формализации игру в период 1 можно изобразить следующим образом:

	Забирать	Не забирать
Забирать	(r, r)	(D, 2r − D)
Не забирать	(2r − D, D)	(Шаг 2)

Для периода 2:

	Забирать	Не забирать
Забирать	(R, R)	(2R − D, D)
Не забирать	(D, 2R − D)	(R, R)

Рассмотрим внимательно матрицу для периода 2. Поскольку и , то в соответствии с принципом последовательной рациональности можем перейти к матрице для периода 1:

	Забирать	Не забирать
Забирать	(r, r)	(D, 2r − D)
Не забирать	(2r − D, D)	(R, R)

Т.к. и , то получаем два равновесия по Нэшу, дающие выигрыши (r, r) и (R, R). Принцип рационализации даёт нам окончательное решение (R, R).