
- •6. Максимин и минимакс игры. Максиминные и минимаксные стратегии. Нижняя и верхняя цены игры в чистых стратегиях. Соотношение между ними.
- •7.Критерий решения игры в чистых стратегиях.
- •8.Доказательство утверждения .
- •9.Удовлетворительность игровой ситуации для игрока a.
- •10.Удовлетворительность игровой ситуации для игрока b.
- •11.Равновесие в антагонистической игре.
- •12.Смешанные стратегии. Функция выигрыша и цена игры в смешанных стратегиях.
- •14.Основная теорема антагонистических игр Джона фон Неймана и седловая точка функции выигрыша.
- •16.Аналитическое решение игры 2×2 в смешанных стратегияхдля игрока b.
- •17.Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока a.
- •18.Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока b.
- •26.Игры с природой. Показатель благоприятности состояния природы. Риск игрока, принимающего решение. Матрица рисков. Принятие решений в условиях риска и неопределённости.
- •27.Критерий Байеса оптимальности чистых стратегий относительно выигрышей.
- •30. Критерий Лапласа оптимальности чистых стратегий относительно рисков.
- •31. Критерий (крайнего пессимизма) Вальда оптимальности чистых стратегий.
- •32. Максимаксный критерий (крайнего оптимизма) оптимальности чистых стратегий.
- •33. Критерий пессимизма-оптимизма Гурвица оптимальности чистых стратегий относительно выигрышей и рисков. Вероятностная интерпретация коэффициентов критерия Гурвица.
- •34. Обобщенный критерий пессимизма-оптимизма Гурвица относительно выигрышей с коэффициентами для смешанных стратегий
- •1) Стратегия pо принадлежит множеству s : pо s;
- •2) Показатель эффективности g(pо) стратегии pо совпадает с ценой игры gs в стратегиях множества s:
- •35. Выбор коэффициентов
- •36. Выбор коэффициентов обобщённого критерия Гурвица для пессимиста.
- •37. Критерий Сэвиджа.
- •38. Критерий Гермейера оптимальности чистых и смешанных стратегий относительно выигрышей.
- •40. Критерий Ходжа – Лемана оптимальности чистых стратегий относительно выигрышей и рисков.
- •41. Основные понятия и определения в теории неантагонистических (бескоалиционных) игр. Способы задания неантагонистической игры.
- •42. Стратегическая форма игры. Чистые и смешанные стратегии игроков в неантагонистических (бескоалиционных) играх. Функции выигрышей игроков. Доминирование стратегий.
- •44. Геометрическое решение биматричных игр 2x2.
- •45. Аналитическое решение биматричных игр 2x2.
- •46.Модель дуополии Курно.
- •47.Модель дуополии Бертрана.
- •48.Модель «Проблема общего».
- •49.Позиционная форма игры.
- •50.Понятие о конечных позиционных играх с совершенной информацией.
44. Геометрическое решение биматричных игр 2x2.
Рассмотрим биматричную игру размерности 2×2:
 .
.
Очевидно, что
смешанные стратегии игроков в случае
игры 2×2 полностью описываются вероятностями
p
и q
выбора игроками своих первых чистых
стратегий. Вторые чистые стратегии
выбираются, соответственно, с вероятностями
1 – p
и 1 – q.
Поэтому, поскольку
 и
и
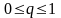 ,
любая ситуация в смешанных стратегиях
в биматричной игре 2×2 может быть
представлена как точка в единичном
квадрате (рис. 8.1).
,
любая ситуация в смешанных стратегиях
в биматричной игре 2×2 может быть
представлена как точка в единичном
квадрате (рис. 8.1).

Рис. 8.1. Графическое
представление ситуации

Ситуациям в чистых стратегиях соответствуют вершины этого квадрата.
Перепишем функцию выигрыша первого игрока в виде
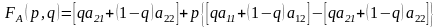 .
.
Ожидаемый выигрыш
первого игрока повышается (в зависимости
от p),
если
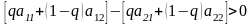 и уменьшается, если
и уменьшается, если
 ,
поэтому лучшими ответами игрока 1 (среди
всех стратегий, как чистых, так и
смешанных), являются
,
поэтому лучшими ответами игрока 1 (среди
всех стратегий, как чистых, так и
смешанных), являются
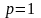 ,
если
,
и
,
если
,
и
 ,
если
.
,
если
.
При
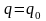 ,
таком, что
,
таком, что
 ,
ожидаемый выигрыш игрока 1 не зависит
от его стратегий. В этом случае игроку
1 безразлично, выбрать ли одну из своих
чистых стратегий, или же выбрать
какую-нибудь смешанную стратегию
,
ожидаемый выигрыш игрока 1 не зависит
от его стратегий. В этом случае игроку
1 безразлично, выбрать ли одну из своих
чистых стратегий, или же выбрать
какую-нибудь смешанную стратегию
 .
Это означает, что если
,
то смешанная стратегия
является наилучшим ответом на смешанную
стратегию
.
Это означает, что если
,
то смешанная стратегия
является наилучшим ответом на смешанную
стратегию
 при любом значении p
от 0 до 1.
при любом значении p
от 0 до 1.
Аналогичные рассуждения можно провести и для второго игрока, основываясь на его функции выигрыша, записанной в виде:
 .
.
Пример.
 .
.
Запишем функцию
выигрыша для первого игрока:
 .
.
Игрок 1 максимизирует
свой выигрыш при
,
если
 ,
или
,
или
 .
Если
.
Если
 ,
или
,
или
 ,
то лучший ответ
.
Если
,
то лучший ответ
.
Если
 ,
первому игроку безразлично, выбрать ли
одну из своих чистых стратегий, или же
выбрать какую-нибудь смешанную стратегию
.
,
первому игроку безразлично, выбрать ли
одну из своих чистых стратегий, или же
выбрать какую-нибудь смешанную стратегию
.
Рассмотрим теперь варианты оптимального по Нэшу поведения игрока 2. Его функцию выигрыша запишем в виде:
 .
.
Игрок 2 максимизирует
свой выигрыш при
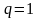 ,
если
,
если
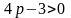 ,
или
,
или
 .
Если
.
Если
 ,
или
,
или
 ,
то лучший ответ
,
то лучший ответ
 .
Если
.
Если
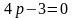 ,
второму игроку безразлично, выбрать ли
одну из своих чистых стратегий, или же
выбрать какую-нибудь смешанную стратегию
,
второму игроку безразлично, выбрать ли
одну из своих чистых стратегий, или же
выбрать какую-нибудь смешанную стратегию
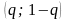 .
.
Теперь найдём точки пересечения построенных графиков, образующие равновесные по Нэшу ситуации.
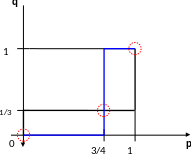
Рис. 8.4. Равновесные по Нэшу ситуации ( черным - 1-й игрок, синим - 2-й)
Таким образом, решение биматричной игры даёт три равновесных по Нэшу игровых ситуаций:
 :
:
 ,
,
 ,
,
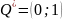 .
. :
:
 ,
,
 ,
,
 ,
,
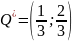 .
. :
:
 ,
,
 ,
,
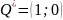 .
.
45. Аналитическое решение биматричных игр 2x2.
Изучение лучших
ответов игроков на поведение противника
позволяет нам сформулировать ещё один
подход к решению биматричных игр. Для
его реализации проверим систему (8.16)
для чистых стратегий игроков, т.е. для
 ,
,
 ,
,
 ,
,
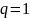 :
:
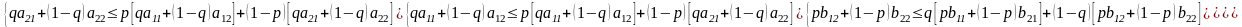
или после алгебраических преобразований

Решение данной системы позволяет находить все равновесные по Нэшу ситуации.
46.Модель дуополии Курно.
Дуополия – это частный случай олигополии, когда на рынке конкурируют друг с другом только 2 фирмы. Две фирмы А и В производят однородный продукт и Q1,Q2 –объемы производства этого продукта. Функция спроса имеет вид P(Q)=a-Q, где Q=Q1+Q2-совокупный объем выпуска продукции фирмами, (P(Q)=0 при Q>=a). Издержки производства у фирм можно записать след. Формулами
C1(Q1)=cQ1
C2(Q2)=cQ2
Функции отражают факт равенства предельных издержек(параметр с) на производство единицы продукции для фирм А и В
Фирмы выбирают Qi одновременно и независимо. Прибыль фирмы равна ее выручке за вычетом издержек производства, то есть формула прибыли является выигрышем игроков.
Πk(Q1,Q2)=Qk(P(Q)-c)=Qk(a-(Q1+Q2)-c), k=1,2
В этой моделе множество стратегий у каждой из 2х фирм не является конечным: каждая фирма может выбрать любой неотрицательный объем производства. Функции выигрышей фирм являются непрерывными функциями от их их стратегий. Если (Q1*,Q2*) –равновесие Нэша, то Qi* должен максимизировать πi
π1(Q1,Q2*)max
π2(Q1*,Q2)max
Решим задачу максимизации прибыли для фирмы А
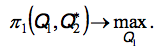
Стоит рассмотреть условия существования экстремума в моделе Курно для игрока А
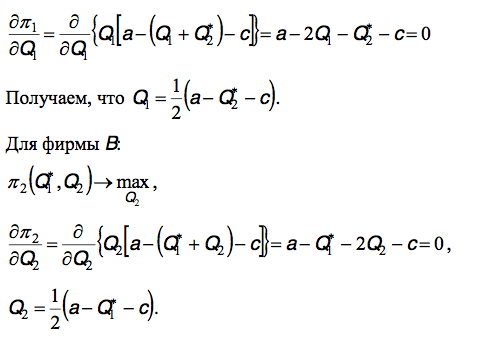
Приравняв Q1*
и Q2*,
мы получим следующее отношение
Q1*=Q2*=1/3(a-c)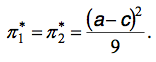
Для графической интерпретации данной игры обозначим функции реакции игроков А и В соответственно символами R1(Q2) и R2(Q1). Таким образом, кривые реагирования будут выглядеть так:
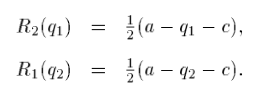 вместо q
надо Q
поставить
вместо q
надо Q
поставить
Ri(Qj) – это объем выпуска i-й фирмы, максимизирующий ее прибыль, при условии, что j-я фирма производит Qj. На графике их также можно изобразить
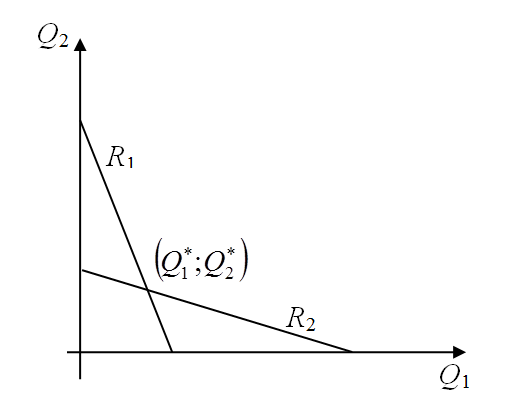 Точка
пересечения кривых реагирования-
равновесие по Курно, то есть равновесие
по Нэшу в модели дуополии по Курно.
Точка
пересечения кривых реагирования-
равновесие по Курно, то есть равновесие
по Нэшу в модели дуополии по Курно.
