3. Расчеты на прочность

1.Определение напряжения. Проверка прочности

Ϭmax = N⁄A≤Ϭadm

2. Определение размера поперечного сечения

А≥N⁄Ϭadm

3. Определение допускаемой нагрузки

N≤AϬadm

3. Статически определимые и статически неопределимые системы

Статически определимыми называются стержневые системы, усилия в которых могут быть определены с помощью уравнений статики.

N1 ∑x = 0, N1 N2

∑y = 0, F N2

N2 F

Получим систему 2хуравнеий с двумя неизвестными. Следовательно, неизвестные усилия могут быть найдены

Получится система двух уравнений с тремя неизвестными, которые не могут быть не найдены.

Системы, все неизвестные которых не могут быть найдены с помощью уравнений статики, называются статически неопределимыми.

Для определения неизвестных используются так называемые уравнения совместимости деформации, которые показывают связь между деформациями.

Разность между количеством неизвестных и количеством уравнений статики называется степенью статической неопределимостью.

3. Изгиб прямых брусьев: основные понятия и определения

Различают поперечный и чистый изгибы.

Поперечным называется изгиб при котором в сечении возникает 2 внутренних силовых фактора Qy и Mz

Чистым называется изгиб при котором в сечении возникает только один внутренний силовой фактор Mz

Изгиб называется плоским, если внешняя нагрузка расположена в плоскости, совпадающей с продольной плоскостью симметрии балки.

При плоском изгибе прогиб балки происходит в плоскости действующей нагрузки.

3. Правила знаков. Дифференциальные зависимости при изгибе

В теории изгиба предусмотрены следующие правила знаков:

- момент считается положительным, если растягиваются нижние волокна, и отрицательным – если верхние

- поперечная сила считается положительной, если действует по часовой стрелке, и отрицательной – если против

3. Нормальные напряжения при чистом изгибе прямых брусьев: основные гипотезы и определения

Основные гипотезы:

1. Продольные волокна не давят друг на друга

2. Сечения плоские до деформации остаются плоскими и перпендикулярными оси стержня после снятия нагрузки (гипотеза плоских сечений – гипотеза Бернулли)

Слой, разделяющий растянутую и сжатую зоны, называется нейтральным слоем.

Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной линией.

3. Нормальные напряжения при чистом изгибе прямых брусьев: вывод формулы через радиус кривизны

-радиус кривизны

Δl=l – l1

По закону Гукка

3. Нормальные напряжения при чистом изгибе прямых брусьев: вывод формулы для определения напряжений в произвольной точке сечения

3. Основная формула в расчетах на прочность при изгибе. Форма эпюр нормальных и касательных напряжений

Основная формула:

3. Осевые и полярные моменты сопротивления

Осевыми моментами сопротивления относительно осей y и z называются величины:

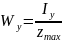
y_max, z_max – расстояние от осей до наиболее удаленных точек сечения

Полярными моментами сопротивления называется величина:

Ρ_max – расстояние от полюса до наиболее удаленных точек сечения

3. Моменты сопротивления прямоугольного поперечного сечения

3. Моменты сопротивления кругового сечения

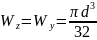
3. Момент сопротивления кольцевого сечения

3. Нормальные напряжения при поперечном изгибе

Основные гипотезы:

1. Поперечное сечение бруса, плоские до деформации остаются плоскими и перпендикулярными к оси бруса после деформации (гипотеза Бернулли)

2. Продольные волокна бруса не давят друг на друга

При поперечном изгибе поперечные сечения искажаются под действием поперечной силы, а продольные волокна давят друг на друга, но это не оказывает заметного влияния на величину и характер распределения нормальных напряжений.

Поэтому при поперечном изгибе нормальные напряжения определяются по тем же формулам, что и при чистом изгибе

Максимальные напряжения (σ max)

При поперечном изгибе нормальные напряжения изменяются по длине балки пропорционально изгибающему моменту

3. Касательные напряжения при изгибе. Формула Журавского

Qy –поперечная сила, Sz – статический момент полусечения относительно Oz

Iz – момент инерции; b(y) – ширина сечения, на уровне которого вычисляется напряжение.

3. Распределение касательных напряжений по высоте различных сечений

A = hb прямоугольное

круговое

A = A^D-A^d

3. Главные напряжения при изгибе

Для плоского напряженного состояния главные напряжения вычисляются по формуле:

Положение площадок, по которым действуют главные напряжения вычисляются по формуле:

Т.к. напряжения τ и σ пропорциональны M и Q, то максимальные главные напряжения возникают в сечениях, где М и Q одновременно имеют максимальные значения

3. Расчет на прочность при изгибе

Подавляющим в большинстве случаев нормальные напряжения больше касательных, поэтому основная проверка на прочность – проверка по нормальным напряжениям.

1. Проверка прочности

основная формула при расчете на прочность при изгибе

Если материал не одинаково сопротивляется растяжению (сжатию) то, проверку прочности следует производить отдельно для каждой зоны

при растяжении

при сжатии

2. Подбор сечения

зная момент сопротивления и форму поперечного сечения можно определить его размеры

3. Определение нагрузки

Если в балке пролет незначителен, то следует провести дополнительную проверку по касательным иглавным напряжениям.

4. Проверка прочности по касательным напряжениям

5. Проверка прочности по главным напряжениям

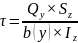
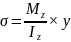
Проверка по главным напряжениям делается в сечении, где Qy и Mz имеют одинаково большие значения