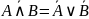1. Вопрос 1 Основные понятия наивной теории множеств.

   1. Понятия множества, его элементов, пустого множества, конечного и бесконечного множеств.

   2. Понятие подмножества. Равенство множеств. Диаграммы Эйлера-Венна.

Множество является основным неопределенным понятием в математике. Под множеством понимают совокупность объектов любой природы, мыслимую как единое целое.

Множество обычно обозначают большими латинскими буквами (А, В, С). Некоторые имеют постоянные обозначения: Натуральные числа, целые числа, рациональные, действительные, числовые промежутки и т.д.

Элементами множества называют объекты его составляющие. Если а-элемент множества А то пишут а А и говорят «а принадлежит А».

Множества, состоящие из n элементов, называются конечными.

Множества, не содержащие ни одного элемента, называются пустыми.

Множества, не являющиеся конечными, называются бесконечными.

Для удобства множества изображают в виде овальных плоских фигур, называемых диаграммами Эйлера – Венна.

При этом элементы множества изображаются точками.

Множество М называется подмножеством множества А если каждый элемент множества М является также элементом множества А. При этом говорят М включается в А или А содержит М. Если множество М может совпадать с А то пишут М А.

По определению: А В<=> хϵА(хϵВ)

(хϵА→хϵВ)

Множества А и В называются равными, если В подмножество А и А подмножество В. При этом пишут А=В

А=В<=>А В A

Пустое множество считается подмножеством любого множества.

2. Способы задания множеств.

   1. Словесное задание.

   2. Перечислением элементов (для конечных множеств)

   3. Указание характеристического свойства.

   4. Порождающая процедура.

Существует несколько способов задания множеств.

1. Словесный

2. Перечислением элементов. Этот способ используется только для конечных множеств. Если множество М состоит из элементов х₁ х₂ …х_k то пишут М={x₁,x₂…x_k}.

3. Указанием характеристического свойства (описание). Некоторое свойство называется характеристическим для множества М, если этим свойством обладают все объекты, принадлежащие множеству М, и не обладает ни один объект, не принадлежащий множеству М. Пусть Р(х) - характеристическое свойство для множества М, тогда пишут М={x|P(x)} или М={x:P(x)}

4. Порождающим правилом или порождающей процедурой. В этом случае способ построения множества описывается некоторой процедурой. М={x|x=f(t)}

3. Операции пересечения и объединения множеств и их свойства.

   1. Определения операций пересечения и объединения множеств.

   2. Доказательство коммутативности и ассоциативности пересечения и объединения множеств.

   3. Доказательство дистрибутивности объединения относительно пересечения и пересечения относительно объединения.

Объединением множеств А и В называется множество, состоящее из всех объектов, принадлежащих хотя бы одному из множеств А и В (т.е. состоящих из всех объектов, принадлежащих А или В). Обозначается А В или А+В.

А В<=>{x|xϵAvxϵB}

Пересечением множеств А и В называется множество, состоящее из всех объектов, принадлежащих как множеству А, так и множеству В. А В (А*В). А В<=>{x|xϵAɅxϵB}.

Коммутативность и ассоциативность пересечения и объединения множеств.

А В=В А, А В=В А – коммутативность

(А В) С=А (В С), (А В) С=А (В С) – ассоциативность.

Дистрибутивность объединения относительно пересечения:

А (В С) = (А В) (А С)

Докажем: а) Пусть хϵАv(В С)=>хϵАvхϵ(В С)=>хϵАv(хϵВɅхϵС)=>

=>(хϵВvхϵА) (хϵАvхϵС)=>хϵ(А В)Ʌхϵ(А С)=>хϵ(А В) (А С)

таким образом множество А (В С) является подмножеством (А В) (А С) и обратно.

Из а) и б) следует, что множества равны.

4. Операция нахождения разности множеств.

   1. Определение разности множеств. Дополнение множества.

   2. Доказательство свойства разности множеств.

   3. Формулировка законов де Моргана.

Разностью множеств А и В называется множество, состоящее из всех объектов, принадлежащих А, но не принадлежащих В.

А\В={х|хϵАɅхнеϵВ}

Если В А, то А\В называется дополнением В до А. Обозначается С_АВ.

С_АВ=А\В, если В А. Если в качестве множества А выступает универсум(универсальное множество), то дополнение В до U называется просто дополнением множества В или абсолютным дополнением множества В. СВ или или Вʽ.

= C_uB

A\B=A

Докажем A\B A и обратно:

x =>x Ʌx =>x Ʌx U\B=>x AɅx =>x A =>A\B A

С\(А В)=(С\А) (C\В)

С\(А В)=(С\А) (C\В)

5. Законы де Моргана.

   1. Определения пересечения, объединения и разности множеств.

   2. Формулировка и доказательство законов де Моргана.

   3. Определение дополнения множества. Следствие законов де Моргана для дополнения множеств.

Объединением множеств А и В называется множество, состоящее из всех объектов, принадлежащих хотя бы одному из множеств А и В (т.е. состоящих из всех объектов, принадлежащих А или В). Обозначается А В или А+В.

А В<=>{x|xϵAvxϵB}

Пересечением множеств А и В называется множество, состоящее из всех объектов, принадлежащих как множеству А, так и множеству В. А В (А*В). А В<=>{x|xϵAɅxϵB}.

Разностью множеств А и В называется множество, состоящее из всех объектов, принадлежащих А, но не принадлежащих В.

А\В={х|хϵАɅх В}

С\(А В)=(С\А) (C\В)

С\(А В)=(С\А) (C\В)

Докажем что С\(А В)=(С\А) (C\В)

хϵС\(А В)<=>xϵCɅx (АvВ)<=>xϵCɅx АɅх В<=>(xϵCɅx А) (хϵСɅх В)<=>

xϵ(C\A) xϵ(C\B)<=>xϵ(C\A) (C\B)<=>C\(A B) (C\A) (C\B)

Если В А, то А\В называется дополнением В до А. Обозначается С_АВ.

С_АВ=А\В, если В А. Если в качестве множества А выступает универсум(универсальное множество), то дополнение В до U называется просто дополнением множества В или абсолютным дополнением множества В. СВ или или Вʽ.

6. Операция нахождения симметрической разности множеств.

   1. Определение симметрической разности множеств.

   2. Формулировка и доказательство свойства симметрической разности.

Симметрической разностью множеств А и В называется объединение множества всех объектов, принадлежащих А, но не принадлежащих В, и множества всех объектов, принадлежащих В, но не принадлежащих А. Другими словами симметрическая разность – множество всех объектов принадлежащих только одному из множеств А и В.

А В=(А B)\(A B) xϵA\B<=>xϵ(A\B) (B\A)<=>(xϵA x В) (xϵB x А)<=>(xϵB xϵA) (x В x А)

<=>xϵ(A B) x (A B)<=>xϵ(A B)\(A B)<=>A B (A B)\(A B)

7. Законы идемпотентности и инволюции.

   1. Перечень основных свойств операций над множествами.

   2. Доказательство законов идемпотентности и инволюции.

1. Коммутативность объединения\пересечения;

2. Ассоциативность;

3. Дистрибутивность объединения\пересечения относительно пересечения\объединения;

4. Свойство идемпотентности;

5. Свойства универсального множества и пустого множества;

6. Эквивалентность;

7. Свойство подмножеств;

8. Свойство Де-Моргана;

9. Свойство симметрической разности;

10. Свойство абсолютного дополнения;

11. Закон инволюции

Идемпотентность: А A=A; A A=A;

Инволюция: =А.

8. Свойства универсального множества, пустого множества, абсолютного дополнения.

   1. Понятия универсального множества и абсолютного дополнения. Понятие пустого множества.

   2. Формулировка и доказательство основных свойств универсального множества и пустого множества.

   3. Формулировка и доказательство свойств абсолютного дополнения.

В случае, если все рассматриваемые множества содержатся в одном и том же множестве U, то множество U называют универсальным или универсумом.

Если В А, то А\В называется дополнением В до А. Обозначается С_АВ.

С_АВ=А\В, если В А. Если в качестве множества А выступает универсум(универсальное множество), то дополнение В до U называется просто дополнением множества В или абсолютным дополнением множества В. СВ или 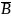или Вʽ.

А U=U

A U=A

A =A

A =

Свойство абсолютного дополнения:

= U

=

A =U

A =

9. Операции над множествами. Приоритеты операций. Принцип двойственности.

   1. Формулировка основных свойств операций над множествами.

   2. Приоритеты операций. Пример.

   3. Принцип двойственности. Пример.

1.Коммутативность. A  B=B  A A  B=B  A 2. Ассоциативность. (A  B)  C=A  (B  C) (A  B)  C= A  (B  C) 3. Дистрибутивность. (A  B)  C = (A  C)  (B  C) (A  B)  C= (A  C)  (B  C) 4. Идемпотентность A  A=A A  A=A 5. Свойства универсального множества и пустого A U = U A UA A  = A A  6.

7. Законы де Моргана 8. Симметрическая разность 9.

9.2 Сначала выполняются операции дополнения, затем пересечения, объединения и разности, которые имеют одинаковый приоритет. Последовательность выполнения операций может быть изменена скобками.

3. Принцип двойственности в абстрактной теории множеств. Пусть дано множество М. Рассмотрим систему всех его подмножеств А, В, С и т. д. Справедливо следующее предложение: если верна теорема о подмножествах множества М, которая формулируется лишь в терминах операций суммы, пересечения и дополнения, то верна также и теорема, получающаяся на данной путём замены операции суммы и пересечения соответственно операциями пересечения и суммы, пустого множества Λ — всем множеством М, а множества М — пустым множеством Λ. При этом дополнение суммы заменяется пересечением дополнений, а дополнение пересечения — суммой дополнений.

10. Мощность объединения конечного числа конечных множеств.

    1. Понятия мощности конечного множества.

    2. Понятия объединения и пересечения множеств.

    3. Число элементов объединения двух и более конечных множеств. Пример.

Мощностью конечного множества называется число его элементов и обозначается n(M).

Объединением множеств А и В называется множество, состоящее из всех объектов, принадлежащих хотя бы одному из множеств А и В (т.е. состоящих из всех объектов, принадлежащих А или В). Обозначается А В или А+В.

А В<=>{x|xϵAvxϵB}

Пересечением множеств А и В называется множество, состоящее из всех объектов, принадлежащих как множеству А, так и множеству В. А В (А*В). А В<=>{x|xϵAɅxϵB}.

Если множества М₁ и М₂ конечны, то имеет место следующая формула:

n(M₁ M₂)=n(M₁)+n(M₂)-n(M₁ M₂)

Формулу можно обобщить на случай 3-х множеств:

n(M₁ M₂ M₃)=n(M₁)+n(M₂)+n(M₃)-n(M₁ M₂)-n(M₁ M₃)-n(M₂ M₃)+n(M₁ M₂ M₃)

В общем случае для любых k-конечных множеств имеет место формула:

n( A_i)=n(A₁)+n(A₂)+…+n(A_k)-n(A₁ A₂) - n(A₁ A₃)-n(A_k-1 A_k)+…

…+(-1)^k-1n(A₁ A₂ … A_k)

Пример:

В группе 36 человек. 25 увлекаются футболом, 20 из них бальными танцами, 10 – и тем, и другим. Есть в группе студенты, которые ничем из этого не занимаются?

11. Разбиение множества на классы.

    1. Понятие дизъюнктивного покрытия некоторого множества.

    2. Число классов разбиения конечного множества. Пример.

Семейство R называется покрытием множества М если объединение всех множеств семейства R совпадает с М, т.е. каждый элемент множества М принадлежит хотя бы одному из множеств семейства R.

R покрытие множества М если ۷М_i=M, M_iϵR, M_i .

Семейство R – дизъюнктивное, если любые два его элемента являются непересекающимися множествами.

R дизъюнктивное если V_i,j(i j=>M₂ M₃= )

Всякое дизъюнктивное покрытие множества М называется разбиением множества М, а его элементы (М_i) – классы этого объединения.

R = {M_i|M_i M} – разбиение М если:

1. M_i

2. Объединение всех M_i совпадает с М.

۷M_i=M

3. Любые 2 элемента семейства R не пересекаются

_i,j(i,j=>M_i M_j= )

В комбинаторике числом Белла B_n называется число всех неупорядоченных разбиений n-элементного множества, при этом по определению полагают B₀ = 1.

Значения чисел Белла B_n для образуют последовательность:

1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, … (последовательность A000110 в OEIS)

Число Белла можно вычислить как сумму чисел Стирлинга второго рода:

Для чисел Белла справедлива также формула Добинского:

.

Числа Белла можно задать в рекуррентном виде:

.

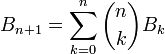Множество из трех элементов {a,b,c} может быть разбито пятью способами: {{a,b,c}}, {{a},{b,c}}, {{b},{a,c}}, {{c},{a,b}}, {{a},{b},{c}} — значит, число Белла B(3) = 5.

12. Понятие бинарного отношения.

    1. Понятие декартова произведения множеств. Пример.

    2. Определение бинарного отношения между элементами двух множеств. Область отправления, область прибытия, область определения и область значения отношения. Пример.

Декартовым (прямым) произведением множеств X и Y называется множество всевозможных упорядоченных пар (x,y) где xϵX, yϵY. Обозначается XxY.

XxY={(x,y)|xϵXɅyϵY}

Бинарным отношением f называется любое подмножество декартового произведения XxY.

Если f бинорное отношение между элементами множеств X и Y то пишут xfy или y=f(x) или (x,y)ϵf и говорят что элемент х находится в отношении f с элементом y, или х и у связаны отношением f или для элементов х и у выполняется отношение f.

Множество всех первых компонент-всевозможных пар из f называется областью определения отношения f и обозначается D(f).

D(f)={xϵX|ƎyϵY(xfy)}

Множество всех вторых компонент-всевозможных пар из f называется областью значения отношения f и обозначается E(f).

E(f) = {yϵY|ƎxϵX(xfy)}

Множество D(f)vE(f) область отношения f.

Множества X и У называются соответственно областью отправления и областью прибытия.

13. Задание бинарных отношений.

    1. Понятие бинарного отношения.

    2. Граф бинарного отношения на конечных множествах. Пример.

    3. Матрица бинарного отношения на конечных множествах. Пример.

Бинарным отношением f называется любое подмножество декартового произведения XxY.

Если f бинарное отношение между элементами множеств X и Y то пишут xfy или y=f(x) или (x,y)ϵf и говорят что элемент х находится в отношении f с элементом y, или х и у связаны отношением f или для элементов х и у выполняется отношение f.

Бинарные отношения на конечных множествах иногда задают графом или матрицей.

Говорят что задан граф отношения f , если на плоскости изображены диаграммы Эйлера-Венна для множеств Х и У и для каждой пары (х,у) из f изображена стрелка, начало которой в точке, изображающей х, а конец в точке, изображающий у. Сами точки х и у вершины графа, стрелки – ребра графа.

Пусть f – бинарное отношение на множествах Х и У, где

х – k-элементное множество, у – m-элементное множество.

Матрица А размера kxm называется матрицей бинарного отношения f, если элементы матрицы удовлетворяют условиям:

a_i,j=1 при x_ify_j

a_i,j=0 при

14. Обратное отношение.

    1. Понятие бинарного отношения и отношения, обратного ему. Пример.

    2. Понятие композиции бинарных отношений. Пример.

    3. Ядро бинарного отношения.

Бинарным отношением f называется любое подмножество декартового произведения XxY.

Пусть f бинарное отношение на множествах Х и У, тогда обратным отношению f называется отношение f^-1, такое что f^-1={(x,y)|yϵY, xϵX, xfy}. Очевидно f^-1 YxX.

Пусть f бинарное отношение на множествах Х и У, ψ – бинарное отношение на множествах Y и Z, тогда композицией отношений называется отношение ψºf такое, что ψºf = {(x,z)|xϵX, zϵZ, ƎyϵY(xfy, yψZ)}.

Ядром отношения f называется композиция f^-1ºf.

15. Композиция бинарных отношений.

    1. Понятие композиции бинарных отношений.

    2. Матрица композиции бинарных отношений как булево произведение матриц исходных отношений. Пример.

Пусть f бинарное отношение на множествах Х и У, ψ – бинарное отношение на множествах Y и Z, тогда композицией отношений называется отношение ψºf такое, что

ψºf = {(x,z)|xϵX, zϵZ, ƎyϵY(xfy, yψZ)}.

Матрица композиции двух отношений

Матрица композиции двух отношений равна логическому произведению матриц исходных отношений.

Матрицы бинарных отношений состоят из логических элементов (1,0) и поэтому должны перемножаться с использованием логических операций сложения (ИЛИ) и умножения (И). В математических пакетах матрицы обычно перемножаются арифметически , что дает дополнительную информацию не только о наличии требуемого маршрута, но и о количестве таких маршрутов.

Пример вычисления матрицы квадрата бинарного отношения

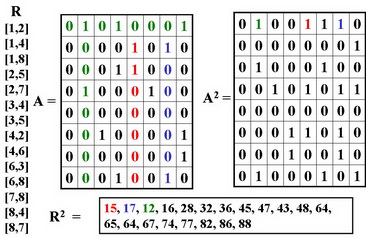
16. Виды бинарных отношений.

    1. Понятие бинарного отношения, заданного на некотором множестве.

    2. Определения видов бинарных отношений.

16.1 Пусть Х и У – некоторое множества.

Бинарным отношением f на множествах Х и У называется любое подмножество декартового произведения.

Если f- бинарные отношения между элементами множеств X и Y, то пишут: xfy или y=f(x) или (x,y)єf и говорят, что элемент х находится в отношении f с элементами у, если х и у связны отношением f, или для элементов х и y выполняется отношение f.

Если множество X=Y=M, то отношение f, заданное на множествах X и Y, называется отношением на множестве М.

16.2 Определение 13.

Отношение f, заданное на множестве М, называется:

-рефлексивным, если для любого xєM(xfx);

-антирефлексивным, если для любого xєM не(xfx);

-симметричным, если для любого x,yєM(xfy→yfx);

-антисимметричным, если для любого x,yєM(xfy,yfx→x=y);

-ассиметричным, если для любого x,yєM(xfy→не(yfx)), т.е. ассиметричность – антирефлексивно – антисимметрично;

-транзитивным, если для любого x,y,zєM(xfy,yfx→xfz);

-связным, если для любого x,yєM(x≠y→xfy v yfx);

Отношение f, заданное на множестве М, называется отношением эквивалентности, если

f – рефлексивно, симметрично, транзитивно.

Отношение f, заданное на множестве М называется отношением порядка, если f – антисимметрично и транзитивно.

Если при этом выполняется связность, то отношение f называется отношением линейного порядка.

Отношение порядка(отношение линейного порядка) называется строгим, если выполняется антирефлексивность. Отношением порядка(отношение линейного порядка) называется не строгим, если выполняется рефлексивность.

17. Классы эквивалентности. Фактор-множество.

    1. Понятие отношения эквивалентности.

    2. Понятие класса эквивалентности, порожденного некоторым элементом.

    3. Фактор-множество. Пример.

Отношение f, заданное на множестве М, называется отношением эквивалентности, если f рефлексивно, симметрично, транзитивно.

Пусть f – отношение эквивалентности на множестве М, а – некоторый элемент множества М, тогда множества К_а={xϵM|xfa} называется классом эквивалентности множества М, порожденным элементом а.

Иногда класс эквивалентности обозначается символом a/f.

Семейство всех классов эквивалентности множества М по отношению к f называется фактор-множеством множества М. Обозначается M/f. Таким образом по определению

M/f={K_a,K_b,K_c….}.

18. Фактор-множество как разбиение множества.

    1. Понятие фактор-множества некоторого множества. Понятие разбиения некоторого множества.

    2. Формулировка и доказательство теоремы о фактор-множестве как разбиении множества.

Семейство всех классов эквивалентности множества М по отношению к f называется фактор-множеством множества М. Обозначается M/f. Таким образом по определению

M/f={K_a,K_b,K_c….}.

Разбиением множества М называется семейство всех его непустых подмножеств, объединение которых совпадает с М, а попарное пересечение пусто.

Фактор-множество непустого множества М по отношению f является разбиением множества М.

1. Покажем, что классы эквивалентности – непустые множества. Пусть К_а – класс эквивалентности, порожденный элементом а, т.е. К_а={xϵM|xfa}.

f – отношение эквивалентности => f – рефлексивно => afa=aϵK_a, таким образом К_а содержит по крайней мере один элемент а.

2. Покажем, что К_аvK_bv…=M.

Обозначим К=K_avK_bv…

xϵK=>xϵK₀=>xϵ{yϵM|yfx₀}=>xϵM=>KϲM

xϵM=>xϵK_x=>xϵK=>MϲK=>K=M, где K_x – класс эквивалентности, порожденный элементом х.

3. Покажем что любые два класса эквивалентности не пересекаются

К_аɅК_в=ø

Предположим противное: ƎсϵМ(сϵКа сϵКв)

f-симметрично сϵК_а=>cfa=>afc, cϵK_b=>cfb=>bfc

f-транзитивно afc, cfb =>afb=>а и в принадлежат одному и тому классу эквивалентности. =>K_a=K_b

Вывод: наше предположение неверно => K_a и К_в – непересекающиеся множества.

М|f – разбиение множества М.

19. Разбиение множества как фактор-множество.

    1. Понятие фактор-множества некоторого множества. Понятие разбиения некоторого множества.

    2. Формулировка и доказательство теоремы о разбиении множества как фактор-множестве.

Семейство всех классов эквивалентности множества М по отношению к f называется фактор-множеством множества М. Обозначается M/f. Таким образом по определению

M/f={K_a,K_b,K_c….}.

Разбиением множества М называется семейство всех его непустых подмножеств, объединение которых совпадает с М, а попарное пересечение пусто.

Любое разбиение R множества М можно рассматривать как фактор-множества множества М по некоторому отношению эквивалентности f.

Пусть R={K₁,K₂…}

То есть

1. K₁

2. K₁ K₂ …=M

3. _i,j(K_i K_j= )

Введем отношение f следующим образом

xfy<=>x и y принадлежат одному и тому же классу разбиения K₀.

Докажем что f-отношение эквивалентности:

1. xfx=>f-рефлексивно

2. xfy=>yfx=>f-симметрично

3. В силу того, что классы разбиения не пересекаются x,yϵK₀=>x,zϵK₀=>f-транзитивно

Таким образом доказана возможность рассмотрения фактор-множества множества М.

Докажем, что R=M/f

К₀ϵR<=> x,yϵK₀(xfy)<=>K₀ϵM/f

Таким образом R=M/f

20. Упорядоченные множества.

    1. Понятие отношения порядка. Частичный порядок. Линейный порядок. Строгий и нестрогий порядок.

    2. Понятие упорядоченного множества.

20.3 Понятие предшествующего и последующего элементов упорядоченного множества. Непосредственные предшественники. Диаграмма Хассе.

20.1 Отношение f, заданное на множестве М, называется:

-отношением порядка, если f одновременно антисимметрично и транзитивно, при этом:

Если f рефлексивно, то отношение нестрого порядка,

Если f антирефлексивно, то отношение строго порядка.

-отношением линейного порядка, если f антисимметрично и транзитивно и связно, при этом:

Если f рефлексивно, то отношение нестрого линейного порядка,

Если f антирефлексивно, то отношение строго линейного порядка,

В случае, когда отношение порядка не является связным, его называют отношением частичного порядка.

20.2 Если на множестве М задано отношение порядка (отношение линейного порядка), то множество М называют упорядоченным (линейно упорядоченным).

20.3 Отношением порядка на множестве М позволяет «сравнивать» между собой различные элементы этого множества.

Определение. Пусть на множестве М задано отношение порядка ≺, тогда если элемент х находится в отношении ≺ с неравным ему элементом у, то х называют элементом, предшествующим элементу у, а у, называют элементом, последующим элементу х.

Определение. Элемент х называется непосредственно предшественником у, если х предшествует у, и не существует таких элементов z, что х≺z и z≺y.

Определение. Диаграммой Хассе называется ориентированный граф, вершины которого – элементы упорядоченного множества, при этом, если х – непосредственным предшественник у, то х располагается ниже у.

20. Вполне упорядоченные множества.

1. Понятие упорядоченного множества.

2. Минимальный и максимальный элементы упорядоченного множества. Число максимальных и минимальных элементов частично упорядоченного множества, линейного упорядоченного множества.

3. Понятие вполне упорядоченного множества. Примеры.

21.1 Если на множестве М задано отношение порядка (отношение линейного порядка), то множество М называют упорядоченным (линейно упорядоченным).

21.2 Определение. Элемент множества М, на котором задано отношение порядка ≺, называется минимальным, если он не имеет предшественником, и максимальным, если он не имеет последующих элементов.

Определение. Упорядоченное множество называется вполне упорядоченным, если любое его подмножество имеет минимальный элемент.

Определение. Пусть Х – подмножество множества М, на котором задано отношение порядка ≺, тогда элемент а є М называется нижней гранью Х, если выполняется условие: для любого х є Х (а ≺ х).

Определение. Пусть Х – подмножество множества М, на котором задано отношение порядка ≺, тогда элемент b є М называется верхней грань Х, если выполняется условие: для любого х є Х (х ≺ b).

21. Ограниченные множества.

    1. Понятия нижней и верхней грани упорядоченного множества.

    2. Точная нижняя и точная верхняя грани множества. Примеры.

22.1 Определение. Наибольшая нижняя грань множества Х(если существует) называется точной нижней гранью множества Х и обозначается inf X.

22.2 Определение. Наименьшая верхняя грань множества Х(если существует) называется точной верхней гранью множества Х и обозначается sup X.

21. Понятие функционального отношения.

    1. Понятие отображения (функции). Образ, прообраз элемента при заданном отображении.

    2. Область отправления, область прибытия, область определения и область значения функционального отношения.

    3. Граф и график функционального отношения.

23.1 Образ, прообраз элемента при заданном отображении.

Пусть f – функция, определённая на множестве Х со значением в У, Х₀ с Х, У₀ с У, тогда множество {f(x)|xєX₀}, называется образом, множество Х₀ при отображении f, а множество {x|f(x)єУ₀} называется прообразом множества У₀ при отображении f.

Множество всех первых компонент-всевозможных пар из f называется областью определения отношения f и обозначается D(f).

D(f)={xϵX|ƎyϵY(xfy)}

Множество всех вторых компонент-всевозможных пар из f называется областью значения отношения f и обозначается E(f).

E(f) = {yϵY|ƎxϵX(xfy)}

Множество D(f)vE(f) область отношения f.

Множества X и У называются соответственно областью отправления и областью прибытия.

23.3 Граф и график функционального отношения.

Граф функционального отношения имеет ребра(стрелки), выход только из одной точки. В графе функционального отношения из одной точки выходит только одно ребро(стрелка).

Если дана функция f : А —» В, где А и В — бесконечные множества,

то граф этого отношения нарисовать не можем. Следует обратиться к традиционной

математической идее графического представления функции, а

именно, ее графику.

21. Композиция функциональных отношений. Обратное отношение.

    1. Понятие функционального отношения.

    2. Композиция функциональных отношений. Пример.

    3. Понятие обратной функции.

Бинарное отношение φ, заданное на множествах X и Y называется отображением X в Y или функциональным отношением, или функцией, если выполняются условия:

, т.е. каждому x ставится в соответствие, при функциональном отношении единственное y.

x – называется независимой переменной, или аргументом, или прообразом y при функции f.

y – называется зависимой переменной, или значением функции, или образом x при функции f.

На случай функционального отношения переносятся понятия области определения, области значения, области отправления, области прибытия, графа, введенные ранее для бинарного отношения. Однако при этом считается, что область отправления совпадает с областью определения, т.е. x=D(f).

Если f определена на множестве X со значением Y, то пишут , или .

Если элементы x и y находятся в отношении f, то кроме записи , используют также запись .