2.2 Ползучесть

Для изучения релаксационных явлений образец быстро нагружают и следят за ходом де­формации растяжения под действием приложенной нагрузки. При этом слож­ность состоит в том, что поперечное се­чение образца со временем уменьшается и таким образом одна и та же нагрузка вызывает в расчете на постоянно умень­шающуюся площадь поперечного сече­ния все

возрастающее напряжение. Су­ществует немало остроумных способов уменьшения действующей силы (груза) по мере растяжения образца, так чтобы сохранить неизменным во времени действующее напряжение. В конечном счете ползучесть осуществляется в режиме σ=const, ε=f(t). На рисунке 2.3 показана типичная кривая ползучести линейного полимера (кривая 1).

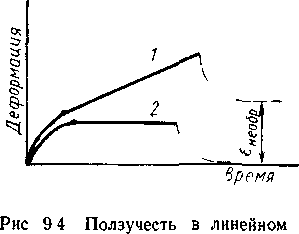
Рисунок 2.3 – Ползучесть в линейном (1) и пространственном полимере.

Под действием нагрузки макромолекулярные клубки развертываются, часть сегментов перемещается, ориентируясь в направлении действия силы. Перемещение сегментов приводит также к смещению клубков относительно друг друга. Таким образом, с самого момента нагружения образца в нем развиваются одновременно и обра­тимая высокоэластическая дефор­мация, и деформация необратимая вязкотекучая.

Если после некоторого времени образец разгрузить, то он частично сократится за счет свертывания клубков макромолекул. Это и будет величина высокоэластической де формации, развившейся к моменту разгрузки

Однако полного сокращения не происходит, сохраняется некоторая остаточная деформация, являющаяся истинно необратимой вязко текучей.

Под действием заданного напряжения клубки макромолекул развернутся тем больше, чем меньше их упругость. Возникшая высокоэластическая деформация далее остается неизменной. Перемещением клубков относительно друг друга течение не прекратится вязкотекучая деформация будет нарастать во времени с постоянной скоростью. Поэтому кривая ползучести делится на два участка начальный криволинейный, когда развиваются оба типа деформации и линейный участок когда накапливается только вязкотекучая деформация. Строго говоря, наличие линейного участка характерно только для полимера с одним временем релаксации. Для реального полимера можно наблюдать участок кривой кажущийся линейным за время наблюдения, но в действтельностни обусловленный различными типами молекулярных перемещений с очень большими временами релаксации.

На том же рис. 2.3 приведена кривая ползучести идеального сетчатого эластомера (кривая 2) в нем не возникает необратимая деформация из за наличия прочных химических связей исключающих взаимное перемещение макромолекул. Эластическая деформация осуществляется лишь в той мере в какой позволяет сетка химических связей ползучесть развивается, достигая предела. После разгрузки образец сокращается до первоначальных размеров.

Основная особенность кривой ползучести — наличие участка замедленного развития упругой деформации. В реальном полимере упругая деформация развивается не мгновенно как в пружине, а замедленно так как перемещение сегментов тормозится вязким сопротивлением среды.

Указанная особенность — наличие замедленной упругости (высокоэластичности) — отображается моделью Кельвина — Фойхта рис. 2.4

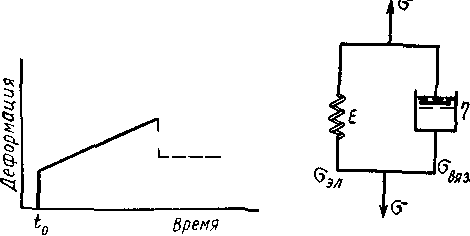
Рисунок 2.4 – Модель Кельвина - Фойхта

Здесь пружина и поршень соединены параллельно напряжения на них складываются . По закону Гука , по закону вязкого

течения Ньютона . В результате , откуда после интегрирования получаем . Это уравнение не предусматривает наличия необратимой деформации поэтому лучше всего моделирует ползучесть пространственно сшитого эластомера. Ползучесть линейного полимера хорошо описывается также объединенной механической моделью сочетающей модель Максвелла и модель Кельвина - Фойхта.