39 Вопрос: Элементы матричного исчисления. Определители матриц.

Пусть дана матрица второго порядка – квадратная матрица, состоящая из двух строк и двух столбцов  .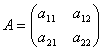

Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом: a₁₁a₂₂ – a₁₂a₂₁.

Определитель обозначается символом  .

Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.

40 Вопрос: Свойства определителей матриц. Минор и алгебраическое дополнение матриц.

Свойство 1. Определитель квадратной матрицы не изменяется при еётранспонировании:

Свойство 2. Если одна из строк (столбцов) матрицы целиком состоит из нулей, то её<#146#>определитель] равен нулю.

Свойство 4. При умножении строки (столбца) матрицы на число её определитель умножается на это число.

Свойство 5. Если каждый элемент i-й строки (столбца) матрицы A представлен в виде суммы двух слагаемых, то определитель такой матрицы равен   , где элементыматриц B и C, за исключением элементов i-й строки (столбца), совпадают с соответствующими элементами матрицы A. A в i-х строках (столбцах) матриц B и C стоят упомянутые первые и вторые слагаемые соответственно.

Минором   элемента   матрицы  n-го  порядка называется определитель матрицы  (n-1)-го порядка, полученный из матрицы  А  вычеркиванием  i-й строки и  j-го столбца.

Алгебраическим дополнением элемента   матрицы   называется число

,

где   — дополнительный минор, определитель матрицы, получающейся из исходной матрицы   путем вычёркивания i -й строки и j -го столбца.

41 Вопрос: Понятие ранга матрицы. Свойства ранга матрицы.

Ранг матрицы - наибольший из порядков ее миноров не равных нулю. Ранг матрицы А обозначают одним из символов: rang А, r. Если все миноры матрицы равны нулю, то ранг ее считается равным нулю.

Из определения ранга матрицы получаем следующие утверждения:

1. Ранг матрицы определяется целым числом, заключенным между 0 и меньшим из чисел m, n.

2. Ранг матрицы равен нулю, если матрица нулевая.

3. Для квадратной матрицы n-го порядка r = п тогда и только тогда, когда матрица невырожденная.

При нахождении ранга матрицы можно пользоваться свойствами миноров. Если все миноры определенного порядка матрицы равны нулю, то все миноры более высокого порядка также равны нулю. Таким образом, если среди миноров порядка k данной матрицы есть отличные от нуля, а всё миноры порядка k + 1 равны нулю или не существуют, то r= k.

Свойства ранга матрицы

1. Ранг матрицы, полученной транспонированием, равен рангу исходной матрицы.

2. Ранг матрицы останется неизменным, если вычеркнуть или приписать нулевую строку (т. е. строку, все элементы которой равны нулю) или нулевой столбец.

При элементарных преобразованиях ранг матрицы не меняется.

42Вопрос: Теорема Кронекера-Капелли.

 Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

RgA = RgA*.