8 Вопрос: Первый и второй замечательные пределы.

Первый замечательный предел:

Второй замечательный предел:

9Впорос: Понятие производной функции.

Если следовать определению, то производная функции в точке — это предел отношения приращения функции Δy к приращению аргумента Δx:

Произво́дная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называетсядифференци́рованием.

Пусть в некоторой окрестности точки   определена функция  Производной функции   в точке   называется предел, если он существует,

Производная функции в точке   обозначается символами

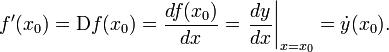
10 вопрос: Геометрический смысл производной функции.

Геометрический смысл производной. На графике функции выбираетсяабсцисса x0 и вычисляется соответствующая ординатаf(x0). В окрестности точки x0выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло серая линия C). Расстояние Δx = x — x0устремляется к нулю, в результате секущая переходит в касательную(постепенно темнеющие линии C). Тангенс угла α наклона этой касательной — и есть производная в точкеx0.

11 вопрос: Производная суммы, разности функций. Производная произведения и частного функций.

Пусть даны функции f(x) и g(x), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:

(f + g)’ = f ’ + g ’

(f − g)’ = f ’ − g ’

Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h)’ = f ’ + g ’ + h ’.

Если есть две функции f(x) и g(x), причем g(x) ≠ 0 на интересующем нас множестве, можно определить новую функцию h(x) = f(x)/g(x). Для такой функции тоже можно найти производную:

Производная произведения считается совсем по другой формуле. А именно:(f · g) ’ = f ’ · g + f · g ’

12Вопрос: Производная сложной функции. Производная обратной функции.

Смотрим в таблицу на правило (№5) дифференцирования сложной функции:

 

Разбираемся. Прежде всего, обратим внимание на запись  . Здесь у нас две функции –   и , причем функция  , образно говоря, вложена в функцию  . Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.

Пусть f : [a, b] → [c, d] непрерывная, строго монотонная на интервале [a, b] функция, имеющая производную в точке х0   [a, b]. Тогда обратная функция g = f -1: [c, d] →[a, b] имеет производную в точке y0 = f(x0) интервала [c, d] равную

,

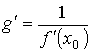если f '(x0) ≠ 0. Если f '(x0) = 0, то g '(y0) = + ∞ (в случае, когда f возрастает), и g '(y0) = − ∞ (в случае, когда f убывает).

13 вопрос: Производные степенных функций, показательных функций, логарифмических функций, тригонометрических и обратных тригонометрических функций.