1Вопрос: Понятие множества. Операции над множествами.

Множество - это совокупность, набор элементов, объединенных общими свойствами.

Множества обозначаются заглавными латинскими буквами   , а элементы множества строчными латинскими буквами   .

Запись   означает, что есть множество   с элементами  , которые связаны между собой какой-то функцией   .

Замечание. Элементы в множество входят по одному разу, т.е. без повторений.

Основные операции:

Принадлежность элемента множеству:

где   -- элемент и   -- множество (элемент   принадлежит множеству   ).

Непринадлежность элемента множеству:

где   -- элемент и   -- множество (элемент   не принадлежит множеству   ).

Объединение множеств:   .

Объединением двух множеств   и   называется множество   , которое состоит из элементов множеств   и   , т.е.

   или

Пересечение множеств:   .

Пересечением двух множеств   и   называется множество   , которое состоит из общих элементов множеств   и   , т.е.

   и

Разность множеств:   .

Разностью двух множеств   и   , например, множество   минус множество   , называется множество   , которое состоит из элементов множества   , которых нет в множестве   , т.е.

   и

Симметрическая разность множеств:   .

Симметрической разностью двух множеств   и   называется множество   , которое состоит из не общих элементов множеств   и   , т.е.

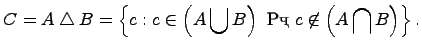
Дополнение множества:   .

Если предположим, что множество   является подмножеством некоторого универсального множества   , тогда определяется операция дополнения:

   и

Вхождение одного множества в другое множество:   .

Если любой элемент множества   является элементом множества   , то говорят, что множество   есть подмножество множества   (множество   входит в множество   ).

Не вхождение одного множества в другое множество:   .

Если существует элемент множества   , который не является элементом множества   , то говорят, что множество   не подмножество множества   (множество   не входит в множество   ).

2Вопрос: Комплексные числа. Геометрический смысл комплексного числа.

Ко́мпле́ксные[1] чи́сла (устар. Мнимые числа[2]), — расширение поля вещественных чисел, обычно обозначается  . Любое комплексное число может быть представлено как формальная сумма  , где   и   — вещественные числа,   — мнимая единица[3].

Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени   с комплексными коэффициентами имеет ровно   комплексных корней (основная теорема алгебры).

Рассмотрим плоскость с прямоугольной системой координат. Каждому комплексному числу   сопоставим точку плоскости с координатами   (а также радиус-вектор, соединяющий начало координат с этой точкой). Такая плоскость называется комплексной. Вещественные числа на ней занимают горизонтальную ось, мнимая единица изображается единицей на вертикальной оси; по этой причине горизонтальная и вертикальная оси называются соответственно вещественной и мнимой осями.

3Вопрос: Понятие функции. Способы задания функций.

Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменная х- независимая переменная или аргумент. Переменная у- зависимая переменная Значение функции- значение у, соответствующее заданному значению х. Область определения функции- все значения, которые принимает независимая переменная. Область значений функции (множество значений)- все значения, которые принимает функция.

Функция является четной- если для любого х из области определения функции выполняется равенство f(x)=f(-x)

Функция является нечетной- если для любого х из области определения функции выполняется равенство f(-x)=f(x)

Возрастающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)<f (х2)

Убывающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)>f(х2)

Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у=f(x), где f(x)- с переменной x. В таком случае говорят, что функция задана формулой или что функция задана аналитически. На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента.