Числовые характеристики выборки.

1. Выборочная средняя.

2. Выборочная дисперсия и среднее квадратическое отклонение.

3. Исправленная дисперсия. Размах, медиана, мода.

4. Примеры расчета числовых характеристик.

1.    Для выборки можно определить ряд числовых характеристик, аналогичных тем, что в теории вероятности определялись для случайных величин. Пусть статистическое распределение выборки объема n имеет вид

Выборочным средним   называется среднее арифметическое всех значений выборки:             1

Выборочное среднее можно записать и так                2

Отметим, что в случае интервального статистического ряда в равенстве в качестве хi  берут середины интервалов, а ni  - соответствующие им частоты. 2.     Выборочной дисперсией  Dв называется среднее арифметическое квадратов отклонений значений выборки от выборочной средней  , т.е.                                                     3 Или то же самое                     4

Можно показать, что дисперсия может быть посчитана по формуле:                             5

Здесь

6 Выборочное среднее квадратическое отклонение выборки определяется формулой 7

Особенность выборочного СКО состоит в том, что оно измеряется в тех же единицах. Что и изучаемый признак. 3.  При решении практических задач помимо использования формул для расчета выборочной дисперсии используется величина, которая называется исправленной выборочной дисперсией. Дело в том, что значение выборочной дисперсии дает заниженные значения по отношению к действительной дисперсии, поэтому при малых выборках (n < 30) необходимо применять исправленную дисперсию и среднее квадратическое отклонение. Эти значения  находятся по формулам 8-9 В качестве описательных характеристик вариационного ряда используется медиана, мода и размах.

• Размахом вариации называется число R = xmax – xmin, где                   10

Xmax -  наибольший из вариант, Xmin  - наименьший из вариант.

• Модой М0* вариационного ряда называется вариант, имеющий наибольшую частоту.

• Медианой Ме* вариационного ряда называется значение признака, приходящегося на середину ряда.

Если объем выборки n – четное число, то               11 Если объем выборки нечетное число, то 

4.  Пример 1. Для примера 1 из предыдущей лекции найти характеристики выборки результатов тестирования 10 абитуриентов:

>Используя формулы 1 -  11 получаем:

1. Среднее значение балла

2. Выборочная дисперсия

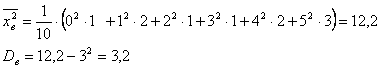
3. Среднее квадратическое отклонение выборки:

4. Исправленная дисперсия

5. Исправленное среднее квадратичное отклонение

6. Размах   R = 5 – 0 = 5.

7. Мода  М0*= 5.

8. Медиана Ме* =  <

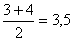Пример 2. Для примера 2 из предыдущей лекции найдите числовые характеристики интервального рядя, построенного в примере. >Используя формулы 1 -  11 получаем:

1. Среднее значение роста

2. Выборочная дисперсия

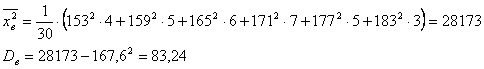
3. Среднее квадратическое отклонение выборки:

4. Исправленная дисперсия

5. Исправленное среднее квадратичное отклонение

Размах, мода и медиана определяются только для дискретных рядов.

25.

Оценки параметров распределения бывают точечные и интервальные.

Пусть   – выборка объема “n”  (1)

Функцию выборки (1)   называют статистикой.

Предположим, что нужно оценить неизвестный параметр  изучаемой случайной величины  .

Def: Статистику  , значения которой близки к оцениваемому параметру  , называют точечной оценкой параметра  .

При   оценка  должна приближаться к параметру  .

Оценка    – случайная величина, поэтому мы не можем потребовать, чтобы оценка стремилась к   в обычном смысле.

Def: Оценка  называется состоятельной, если при  в вероятностном смысле стремится к  .

 – обычная сходимость.

Поскольку оценка    – случайная величина, то рассмотрим ее математическое ожидание

.

Def: Оценка  называется несмещенной, если ее математическое ожидание совпадает с оцениваемым параметром  :  .

Несмещенная оценка с минимальной дисперсией называется эффективной.

Основные оцениваемые параметры распределения:

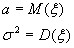
Построим точечные оценки для этих параметров.

Точечную оценку для “a” называют выборочное среднее.

Точечную оценку для  называют выборочная дисперсия.

2ой вопрос не нашёл.

26.

Интервальное оценивание — один из видов статистического оценивания, предполагающий построение интервала, в котором с некоторой вероятностью находится истинное значение оцениваемого параметра.

Пусть   - неизвестный параметр генеральной совокупности. По сделанной выборке по определенным правилам находятся числа   и   такие чтобы выполнялось неравенство:

Интервал   является доверительным интервалом для параметра  , а число   - доверительной вероятностью или надежностью сделанной оценки. Обычно надежность задается заранее, причем выбираются числа близкие к 1 (0.95, 0.99 или 0.999).

Доверительный интервал и доверительная вероятность

Рассматривая характеристики нормального распределения, мы уже отмечали, что вероятность появления погрешности, не выходящей за пределы +/-,s составляет 0,6826. В этом случае +/-s рассматривается как граница интервала, в пределах которой с указанной вероятностью лежит отклонение дельта. При нормальном распределении вероятность попадания случайной величины в интервал от -Е до +Е выражается формулой: , где при t>0 Ф(t) называется интегралом Лапласа или доверительной вероятностью, соответствующей доверительному интервалу +/-Е, а величину 1 – Ф(t) – уровнем значимости. Обычно доверительную вероятность выбирают исходя из конкретных условий. Например, для изготовления какой-либо детали можно считать удовлетворительным значение 0,995 для вероятности того, что отклонение размера не выйдет за пределы заданного интервала. В технике вероятность выражают в процентах – 99,5%. Соответственно, уровень значимости или вероятность того, что детали не будут удовлетворять данному требованию, 0,5%. Это означает, что в среднем будет отбракована 1 деталь из 200. Такая вероятность соответствует доверительному интервалу +/- 2,81. Часто пользуются «правилом трех сигм», т.е. доверительным интервалом +/-3s, для которого доверительная вероятность составляет 99,73%. На этом основании можно сформулировать следующее правило: если при многократном измерении одной и той же физической величины постоянного размера сомнительное значение результата измерения отличается от среднего значения больше чем на 3s, то с вероятностью 0.997 оно является ошибочным и его следует отбросить. Это правило называется «правилом трех сигм».