9. Локальная теорема Муавра-Лапласа

Пусть 0< p <1 и величина   при n    ограничена. Тогда  .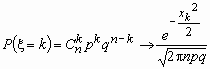

На практике приближением Муавра-Лапласа пользуются при npq > 9.

Точность формулы 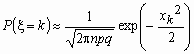  растет, как с ростом величин n и k, так и по мере приближения величин p и q к 0.5.

Интегральныя теорема Лапласа

Пусть производится п испытаний, в каждом из которых вероятность появления события А постоянна и равна р (0<p<1). Как вычислить вероятность P_n(k₁, k₂) того, что событие А появится в п испытаниях не менее k₁ и не более k₂ раз (для краткости будем говорить «от k₁ до k₂ раз»? На этот вопрос отвечает интегральная теорема Лапласа.

Теорема. (Интегральная теорема Лапласа). Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(k₁, k₂) того, что событие А появится в п испытаниях от k₁ до k₂ раз, приближенно равна определенному интегралу:

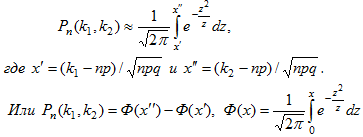 - интегральная функция Лапласа.

14.

Геометрическое распределение. Дискретная случайная величина Х имеет геометрическое распределение, если ее возможные значения 0, 1, 2, ... , m, … , а вероятности этих значений:

          

где 0 < p < 1,  q = 1 – p ;  m = 0, 1, 2, ... .

Вероятности Рm для последовательных значений m образуют геометрическую прогрессию с первым членом р и знаменателем q, откуда и название «геометрическое распределение».

В качестве примера рассмотрим стрельбу по некоторой цели до первого попадания, причем вероятность попадания при каждом выстреле не зависит от результатов предыдущих выстрелов  и сохраняет постоянное значение р (0 < p < 1). Тогда количество произведенных выстрелов будет случайной величиной с геометрическим распределением вероятностей. 

Геометрическое распределение определяется одним параметром р. Cлучайная величина, подчиненная геометрическому закону распределения, имеет следующие основные числовые характеристики:

           

21.

Генеральная совокупность и выборка из нее

Основу статистического исследования составляет множество данных, полученных в результате измерения одного или нескольких признаков. Реально наблюдаемая совокупность объектов, статистически представленная рядом наблюдений  случайной величины  , является выборкой, а гипотетически существующая (домысливаемая) — генеральной совокупностью. Генеральная совокупность может быть конечной (число наблюдений N = const) или бесконечной (N = ∞), а выборка из генеральной совокупности — это всегда результат ограниченного ряда   наблюдений. Число наблюдений  , образующих выборку, называется объемом выборки. Если объем выборки   достаточно велик (n → ∞) выборка считается большой, в противном случае она называется выборкой ограниченного объема. Выборка считается малой, если при измерении одномерной случайной величины   объем выборки не превышает 30 (n <= 30), а при измерении одновременно нескольких (k) признаков в многомерном пространстве отношение n к k не превышает 10 (n/k < 10). Выборка образует вариационный ряд, если ее члены являются порядковыми статистиками, т. е. выборочные значения случайной величины Х упорядочены по возрастанию (ранжированы), значения же признака называются вариантами.