Глава 14

ЭВРИСТИЧЕСКИЕ МЕТОДЫ

14.1. Эвристический подход к выбору вариантов

Достаточно широкое распространение на практике получи­ли эвристические методы рационального выбора, основанные на функциональной модели в виде действительной функции, кото­рая характеризует в случае определенности ценность или в случаевероятностной неопределенности полезностьва­рианта . для ЛПР.

Предполагается, что ЛПРможет оценить ценность/полез­ность каждого варианта по многим количественным критериям с помощью частных числовых функций ценности Общая ценность варианта либо количественно оценивается непосредственно самим ЛПР или группой экспертов, либо тем или иным обра­зом вычисляется, используя полученную от ЛПР информацию. При этом никак не обосновывается ни вид общей функциональ­ной зависимостиценности от оценок по частным критериям, ни способы измерения входящих в функцию показателей.

Сопоставление каждому варианту его числовой ценности позволяет ЛПР очень просто проводить сравнение вариан­тов по предпочтительности: вариант предпочтительнее вари­анта тогда и только тогда, когда , и варианты равноценны , если

Сравнивая варианты по их ценности , можно упоря­дочить варианты или найти лучший вариант, имеющий макси­мальную ценность.

Если задана ранжировка вариантов

то функция ., где — ранг варианта , опре­деляемый формулой (3.1), является одной из простейших функ­цией ценности. Действительно, если ■

В зависимости от способа определения общей ценности вари­анта выделим группы методов прямой оценки вариантов:

1. вычисление общей ценности по заданной формуле;

2. поиск компромисса между отдельными частными ценно­стями.

14.2. Вычисление общей ценности по заданной формуле

Вычисление общей ценности варианта как некоторо­го функционала

зависящего от многих частных функций ценности вид

которого и все его параметры задаются ЛПР или экспертами, является одним из самых популярных эвристических подходов, широко применяемым на практике.

Часто общая функция ценности задается с помощью адди­тивной свертки частных функций ценности в виде так назы­ваемой взвешенной суммы

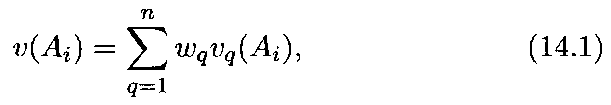
с помощью мультипликативной свертки

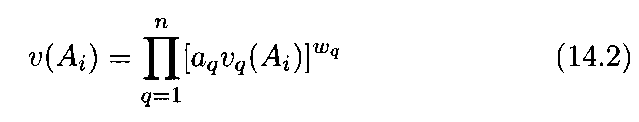
или аддитивно-мультипликативной свертки в виде полили­нейной функции

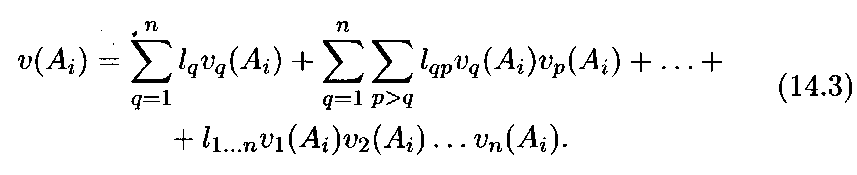
Здесь — вес q-го критерия, характеризующий его важ­

ность или значимость для ЛПР; — шкалирующие

коэффициенты. Числовые значения " " могут либо на­

значаться непосредственно ЛПР, либо рассчитываться по неко­торой процедуре на основе оценок ЛПР. Обычно при аддитив­ной свертке считается, что веса частных критериев нормирова­ны условием

Во многих задачах выбора задается простейший вид частной функции ценности полагая ее просто равной число­

вой оценке варианта по q-му частному критерию

Когда оценки варианта измеряются целыми числами, а все веса метод взвешенной суммы называют балльным

методом. В иных случаях полагают

Типичными примерами общей функции ценности для п = 2 являются:

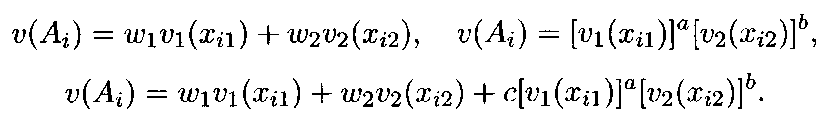
Часто удобно перейти к величинам нормированным в преде­лах воспользовавшись, например, преобразованием

d ряде методов функция оощей ценности варианта вводится в виде так называемой штрафной функции, оценивающей откло­нение от заданных параметров, например от лучших значений по частным критериям:

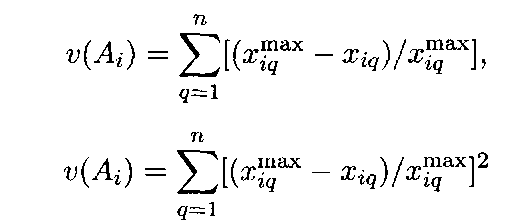
или от худших значений

Для аргументации вывода о справедливости той или иной формулы, задающей общую функцию ценности варианта, обыч­но ссылаются на выполнение определенных условий, анало­гичных используемым в методах многокритериальной оптими­зации. В их числе могут выступать принципы равномерно­сти, справедливого компромисса, выделения главного крите­рия, установления допустимых уступок и допустимых порого­вых уровней, указания предельно возможных оценок (уровней притязания, идеальных точек) и др.

Так, при объяснении использования аддитивной свертки частные ценности трактуются как «весомость» отдельных со­ставляющих некоторого целого. Применение мультипликатив­ной свертки объясняют тем, что частные ценности можно ассо­циировать с вероятностями достижения определенных целевых показателей. Однако во всех этих случаях, в том числе и в рас­смотренных выше, ЛПР достаточно трудно обосновать выбор вида общей зависимости функции ценности от частных крите­риев, а сам выбор также не является однозначным.