Часть III

ИНДИВИДУАЛЬНЫЕ РАЦИОНАЛЬНЫЕ РЕШЕНИЯ

Глава 13

РАЦИОНАЛЬНЫЙ ВЫБОР

13.1. Понятие рационального выбора

Одним из краеугольных камней современной теории приня­тия решений служит постулат рациональности (от лат. ratio — разум) предпочтений человека при индивидуальном выборе луч­шего варианта. Считается, что каждый человек должен иметь свое собственное (реальное или воображаемое, явное или неяв­ное) представление о ценности сравниваемых вариантов, свой собственный «измеритель ценности». И ЛПР, делая свой выбор, интуитивно или осознанно стремится получить в конечном итоге наиболее выгодный для себя результат. Тем самым в понятие ра­ционального выбора включается так или иначе понимаемое по­нятие оптимальности, хотя само это понятие уже не является определяющим.

Рациональность выбора предполагает также его субъектив­ность. Вариант решения, наилучший или приемлемый для од­ного, может не быть таковым для другого. У каждого челове­ка есть свои собственные предпочтения, на основании которых он сравнивает варианты и выбирает из них наиболее предпочти­тельный для себя вариант. С необходимостью учета субъектив­ных предпочтений ЛПР при выборе лучшего варианта мы уже сталкивались в задачах многокритериальной оптимизации и ве­роятностного выбора.

Использование полученной от ЛПР информации о различ­ных аспектах сравниваемых вариантов в процедурах исклю­чения и компенсации критериев позволяет последовательно сужать область допустимых значений переменных и в ряде слу­чаев находить наилучшие решения задачи. Аналогичные проце­дуры исключения и компенсации критериев широко использу­ются и при рациональном выборе. Сначала из имеющегося мно-

жества вариантов тем или иным образом выделяется подмноже­ство недоминируемых вариантов, а затем это подмножество по­следовательно сужается с учетом предпочтений ЛПР.

Вместе с тем ЛПР, как и любой человек, может вести се­бя непоследовательно, ошибаться в своих оценках и выводах, противоречить самому себе. Подобное поведение обусловлено различными причинами, в частности трудностью анализируе­мой ситуации, недостатком и/или недостоверностью имеющей­ся информации, дефицитом времени, недостаточной опытно­стью человека и/или ограниченностью его мышления, непред­намеренным заблуждением, усталостью и невнимательностью, индивидуальными склонностями человека завышать или зани­жать свои оценки, рисковать или быть осторожным в суждениях и т. п. Считается, что такого рода ошибки и противоречия не со­гласуются с понятием индивидуальной рациональности и пото­му должны выявляться и устраняться в процессе решения зада­чи. В то же время при групповом принятии решения необходимо стремиться к компромиссу при агрегировании несовпадающих предпочтений нескольких ЛПР.

13.2. Задача рационального выбора

Задачи рационального выбора обычно возникают в уникаль­ных и повторяющихся проблемных ситуациях, обладающих осо­бенностями плохо структурируемых проблем, а именно:

1.отсутствует формализованная модель проблемной ситуа­ции, которую бывает трудно или невозможно построить из- за сложности ситуации, отсутствии необходимой информации и т. п.;

2.имеется большая неопределенность при формировании пе­речня всех возможных вариантов решения проблемы, а сами ва­рианты могут описываться и количественными, и качественны­ми показателями с преобладанием последних;

3.отсутствуют одинаково понимаемые и формализуемые кри­терии для сравнения и выбора вариантов;

4.наиболее предпочтительный (наилучший) результат выбо­ра определяется субъективными предпочтениями ЛПР.

Задача рационального выбора состоит в следующем. Имеется несколько реально существующих или гипотетически возмож­ных вариантов (объектов, альтернатив) число кото­рых может быть как конечным, так и бесконечным. Варианты заданы изначально или могут появляться в процессе решения за-

дачи. Каждый вариант оценивается по единственному или мно­гим критериям имеющим числовые или вербальные, непрерывные или дискретные шкалы оценок

Порядковые шкалы обычно предполагаются упо­рядоченными, например от лучших градаций оценок к худшим. Варианту сопоставляется n-мерный вектор или кортеж оце­нок либо одна или п целевых функций

— оценка варианта по q-му критерию Совокупности вариантов соответствует допустимое множе­ство

Основываясь на предпочтениях ЛПР и используя всю имею­щуюся информацию, требуется решить одну из следующих за­дач: 1) выделить лучшие варианты; 2) упорядочить все вариан­ты от лучшего к худшему; 3) отнести каждый вариант к одному из заранее указанных классов решений. Главная сложность при решении задачи рационального выбора заключается в выявле­нии и формализации предпочтений ЛПР.

Модель рационального выбора отражает предпочтения кон­кретного ЛПР и тем самым всегда носит субъективный харак­тер. Эта модель может иметь формализованное представление и состоять из некоторых определенных требований или правил описания вариантов, процедур их сравнения и выделения луч­ших вариантов, может задаваться функциональными зависимо­стями либо быть неформальной. Обычно предполагается, что для вариантов выполняется условие постоянства свойств, или аксиома независимости от посторонних вариантов, а именно: оценки каждого варианта и/или результаты сравнения двух ва­риантов не должны зависеть от наличия или отсутствия других вариантов.

В ряде случаев задается условие независимости критериев по предпочтению, устанавливающее независимость результатов попарного сравнения вариантов по отдельным кри­териям от одинаковых оценок по другим критериям. Это усло­вие состоит в следующем. Пусть два варианта различаются оценками по некоторому критерию причем а по

остальным критериям оценки вариантов совпадают. Если из до­минирования векторов/кортежей оценок

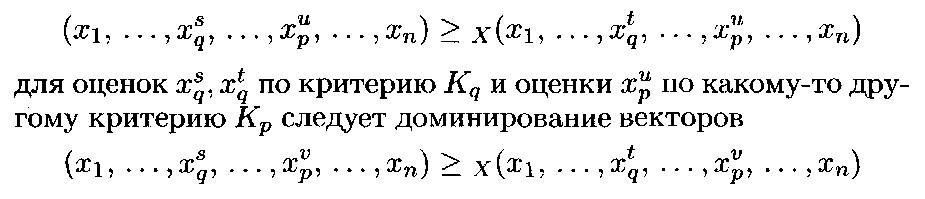
для всех других оценок и любых критериев

то критерий называется независимым по предпочте­нию от остальных критериев. Здесь знаком обозначено отно­шение доминирования и векторов, и кортежей.

Имеются разные подходы к формализации модели рацио­нального выбора. Одной из наиболее распространенных явля­ется функциональная модель рационального выбора, выражае­мая монотонной действительной функцией ценности или полез­ности, которая достигает минимального и максимального зна­чений на множестве допустимых вариантов. Лучшим считается тот вариант, чья полезность выше. Тот или иной вид функции полезности определятся аксиомами общего характера и аксио­мами рациональности суждений ЛПР. В теории экономическо­го поведения Дж. фон Неймана и О. Моргенштерна (1944) по­стулируется аксиоматика, обеспечивающая существование чис­ловой функции, которая ассоциируется с мерой потребитель­ских благ для ЛПР. П. Фишберн доказал (1964), что если на конечном множестве вариантов задан строгий слабый порядок (асимметричное и отрицательно транзитивное отношение), то существует аддитивная действительная функция, определяю­щая многомерную ценность (в случае определенности) или по­лезность (в случае неопределенности) вариантов. Аналогичное утверждение для бесконечного множества вариантов было дока­зано Г. Дебрё (1959). Ясно, что такая функция не является един­ственной.

Вместе с тем, как оказалось, не всегда возможно построить функциональную модель рационального выбора, которая и вы­ражает, и-количественно измеряет качество варианта. На прак­тике и в многочисленных экспериментах было обнаружено, что принимаемые людьми решения не всегда соответствуют тем или иным аксиомам рациональности. Нередко люди ведут себя непо­следовательно, противоречиво, прибегают при выборе к различ­ным эвристикам.

Поэтому были предложены иные модели рационального вы­бора, не использующие понятие числовой функции ценности или полезности. Сформулированная Б. Руа аксиома ограниченной сравнимости (1968) позволяет сравнивать варианты, имеющие многокритериальные числовые оценки, по отношению к огра­ниченной пороговой предпочтительности. При этом допускается существование некоторых зон неопределенности, отличающихся оценками по критериям, в пределах которых предпочтения ЛПР сохраняют свой характер.

В методах вербального анализа решений, разработанных О. И. Ларичевым и другими, рациональность индивидуума озна­чает транзитивность и непротиворечивость его суждений, кото­рые проверяются по результатам многократных сравнений вари­антов, отличающихся своими многокритериальными оценками на вербальных порядковых шкалах. Для построения решающих правил выбора применяются только такие операции преобразо­вания информации, которые сохраняют качественный характер данных и допустимы с точки зрения их выполнимости челове­ком.

В теории функций выбора сужение исходного множества вариантов до небольшого числа приемлемых осуществляется по определенным правилам с учетом имеющейся информации о свойствах вариантов и предпочтениях ЛПР. Возможность конструирования разнообразных механизмов выбора позволяет описывать как классически рациональные, так и иные модели выбора, допускающие, в частности, нетранзитивность предпо­чтений и отказ от выбора.