Постановка задачи

Пусть есть функция  .Требуется найти корень этой функции: такой   при котором  Решение необходимо найти численно, то есть для реализации на ЭВМ. Для решения этой задачи предлагается использовать метод простых итераций.

Метод простых итераций в общем виде

Заменим исходное уравнение   на эквивалентное  ,и будем строить итерации по правилу  . Таким образом метод простой итерации - это одношаговый итерационный процесс. Для того, что бы начать данный процесс, необходимо знать начальное приближение  . Выясним условия сходимости метода и выбор начального приближения.

Сходимость метода простых итераций

Метод сходится, если при   последовательность { } имеет предел.Обозначим   окресность точки   радиуса  , то есть  .Теорема 1. Если   липшиц-непрерывна с константой   на  , то есть выполняется

,

при этом если также выполнено

,

то уравнение   имеет единственное решение на   и метод простой итерации сходится к решению при любом выборе начального приближения  .Так же справедлива оценка:

,

где   - точное решение.Из оценки видно, что метод линеен. Пусть   непрерывно дифференцируема на  , тогда из теоремы вытекают следующие утверждения:Следствие 1. Если   для  , выполнено  , и  , тогда уравнение   имеет единственное решение на   и метод простой итерации сходится к решению.

Следствие 2. Если уравнение   имеет решение  ,   непрерывно дифференцируема на   и  . Тогда существует   такое, что на   уравнение не имеет других решений и метод простой итерации сходится к решению при 

Геометрическая интерпретация

Рассмотрим график функции  . Это озночает, что решение уравнения   и   - это точка пересечения   с прямой  :

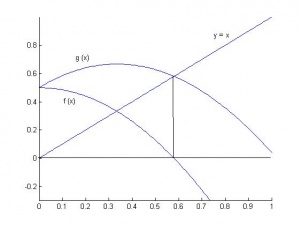
И следующая итерация   - это координата   пересечения горизонтальной прямой точки   с прямой  .

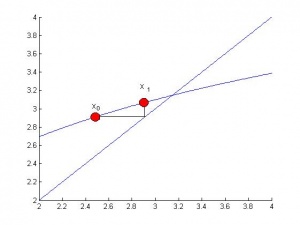Из рисунка наглядно видно требование сходимости  . Чем ближе производная   к  , тем быстрее сходится алгоритм. В зависимости от знака производной вблизи решения приближения могут строится по разному. Если  , то каждое следующее приближение строится с другой стороны от корня:

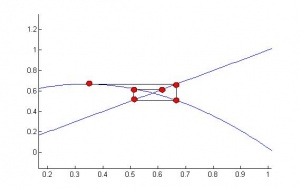
Билет 7 Процедурный тип

В программировании часто встречается ситуация, когда в алгоритме используется результат вычисления некоторой функции, но сам алгоритм не зависит от того, какая именно функция вычисляется. В языке Turbo Pascal можно описать и использовать так называемый процедурный тип данных. Описание процедурного типа состоит из слова procedure или function, за которым в круглых скобках записывается список формальных параметров. Для функции после списка формальных параметров через двоеточие указывается тип функции. После того, как определен процедурный тип, можно описать переменные процедурного типа. Переменным процедурного типа можно присваивать значения конкретных процедур и функций. Естественно, что процедурная переменная и та процедура, которая присваивается ей в качестве значения, должны иметь одинаковое число формальных параметров, совпадающих по типам. Если переменная имеет тип функции, то для функций кроме формальных параметров должны совпадать типы функций. Те процедуры и функции, которые будут использоваться либо в качестве значений для процедурных переменных, либо в качестве фактических параметров при вызове процедур и функций, должны удовлетворять следующим правилам:

-должны компилироваться с ключом компилятора {$F+}

-не должны быть стандартными процедурами или функциями

-не должны объявляться внутри других процедур или функций

С погрешностью 0.0001 методом простой итерации уточнить корни уравнений ln(x)- x +1.8 = 0 на отрезке [1; 3] и 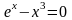на [0; 2].

Текст программы

program lab12;

const e = 0.0001;

type tip = function (x : real): real; { Процедурный тип}

{$F+} { Директива дальней компиляции}

function f1(x : real) : real;

begin f1 := ln(x) - x + 1.8 end;

function pf1(x : real) : real;

begin pf1 := 1/x – 1 end;

function f2(x : real) : real;

begin f2 := exp(x) - x*x*x end;

function pf2(x : real) : real;

begin pf2 := exp(x) - 3*x*x end;

{$F-} { Отмена директивы}

function Koren(a, b : real; f, pf : tip) : real; { Основная подпрограмма}

var x : real;

begin x := (a + b)/2; {Начальное приближение}

repeat

x := x - f(x)/pf(x)

until abs(f(x)) < e;

Koren := x

end;

begin

writeln('Корень уравнения ln(x)-x+1.8 на отрезке [1; 3] : ', Koren(1, 3, f1, pf1):6:4);

writeln('Корень уравнения exp(x)-x*x*x на отрезке [0;2] : ', Koren(0, 2, f2, pf2):6:4);

readln

end.

Сортировка символьных данных

Понятие: сортировка символов сводится к сравнению кодов этих символов и принятие соответствующих мер. Сортировка строк, имхо, сложнее, поскольку имеем два варианта, например: яблоко - книга ----> я>к при сравнении кодов я и к. книга - камень ----> к=к, далее н<а и т. д. Пример: сортировка символов по возрастанию (брал именно символы, чтобы легче было разобраться)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

uses crt; var i,j,l,min:integer; //переменные-счетчики, min - для сортировки     r:char; // вспомогательная переменная для обмена элементов a:array [1..10] of char; //массив со словами или символами. я использовал символы, чтобы упростить задачу begin      clrscr;      writeln('Ввод слов, символов');      for i:=1 to 10 do          begin               write(i,' - ');               readln(a[i]);          end;                            //ввод-вывод исходных данных      writeln('Исходный массив');      for i:=1 to 10 do          write(a[i],' ');      writeln;      //алгоритм сортровки. начало      for i:=1 to 10 do          begin               min:=ord(a[i]);               for j:=i to 10 do                   if ord(a[j])<min then //сравнение кодов элементов по таблице windows                      begin                           min:=ord(a[j]);                           l:=j;                      end;               r:=a[i];               a[i]:=a[l];     //ставим элемент с наименьшим кодом на первое место относительно i (если i=2, то превое место - 2 и т. д.)               a[l]:=r;          end;      //конец алгоритма      writeln('Результат: ');      for i:=1 to 10 do          write(a[i],' '); end.

Билет №8

Нетипизированные параметры.

При описании нетипизированных параметров не указывается тип. Передаются они всегда по адресу - либо как константы, либо как переменные, например:

procedure P(const a, b; var y);

Есть одно важное ограничение: передать-то их можно, а вот делать с ними в подпрограмме что-либо до тех пор, пока они не приведены к какому-то определенному типу, все равно нельзя!

Явное преобразование типов

В ряде случаев в Pascal происходит автоматический переход от одного типа данных к другому (от целого к действительному, от символьного к строковому и т.д.). Существует также ряд функций, осуществляющих преобразование типов (ord, chr, trunc, round). Наряду с этим в Паскаль возможно явное преобразование типов (ретипизация данных). Для того, чтобы осуществить явное преобразование типа, необходимо использовать имя типа аналогично тому, как используется имя функции. В качестве параметра в этом случае указывается имя преобразуемой переменной.

Преобразовать можно любой тип к любому другому, однако следует выполнять требование: в операторе присваивания переменная слева должна занимать в памяти столько же или больше байт, сколько занимает преобразуемое значение.