Вопрос 6. Вероятность появления хотя бы одного из n событий, независимых в совокупности.

Вероятность появления хотя бы одного из n событий, независимых в совокупности равна разности между единицей и произведением вероятностей противоположных событий

Р( )=1- , (7), где - вероятность противоположного события

Доказательство: Т.к. событие и противоположны, то I их вер-тей равна 1 Р( )=1- Р( )=1- .

Следствие: Если события имеют равные вер-ти q( )=q, то вер-ть наступления хотя бы одного из них : Р( )=1- (8)

Вопрос 7. Теорема сложения вероятностей совместных событий. Вероятность наступления только одного, хотя бы одного события.

Р(А+В)=Р(А)+Р(В)-Р(АВ) (9)

А+В= +АВ+ В-несовместимы

Р(А+В)=Р(А )+Р(АВ)+Р( В) (*)

Очевидно, что А= А +АВ

Р( В)=Р(А)-Р(АВ) (**)

В= В+АВ

Р( В)=Р(В)-Р(АВ) (***)

(**) и (***) подставим в (*)

Р(А+В)=Р(А)-Р(АВ)+Р(АВ)+Р(В)-Р(АВ)=Р(А)+Р(В)-Р(АВ)

Вопрос 8. Формула полной вероятности и формула Байеса

Если события образуют полную группу, то для вычисление вероятности произвольного события А можно использовать формулу полной вероятности

Р{A}=P{A|H1}P{H1}+ P{A|H2}P{H2}+…+ P{A|Hn}P{Hn}= P{A|Hi}P{Hi}

В соответствии с которой вероятность наступления события А может быть представлена как сумму произведений условных вероятностей события А при наступлении событий Нi на безусловные вероятности этих событий Нi . Поскольку среди событий , образующих полную группу, в результате опыта должно наступить одно и только одно, эти события Аi называют гипотезами ( ). Формула полной вероятности остается справедливой и в случае, если условие состоящее в том, что события образуют полную группу, заменить более слабым: гипотезы ( ) попарно несовместимы ( , ), а их объединение содержит событие А( ).

Из формулы полной вероятности следует формула Байеса

Вероятности гипотезы называют априорными вероятностями (вероятностями гипотез до проведения опыта) в отличие от апостериорных вероятностей ( вероятностей гипотез уточненных в результате опыта исходом которого стало событие А )

Вопрос 9. Понятие дискретной случайной величины и ее з-на распределения. Многоугольник распределения.

СВ называется дискретной, если множество ее возможных значений конечно или счётно. Например, число бросаний монеты до появления герба или число выпавших очков при бросании игрального кубика.

Для полного задания СВ необходимо указать множество ее возможных значений и определить некоторое соответствие между отдельными ее значениями x_i (или некоторыми подмножествами) и вероятностями p_i, с которыми эти значения (или подмножества) принимаются, для СВДТ достаточно указать зависимость p_i = P{X = x_i} или таблицу. Так же ставят в соответствие вероятности не отдельные значения СВ, а множество значений (X < x), где x – произвольное число

Вопрос 10. Функция распределения случайной величины и её свойства.

Функцией распределения (ФР) (или интегральным законом распределения) СВ X называется числовая функция F(x) = P{X < x}, определенная для любых x  R. Свойства ФР:

1. 0  F(x)  1;

2. F(x₁)  F(x₂), если x₁  x₂, т.е. F(x) - неубывающая функция;

3. 

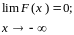
4. P{a  X  b} = F(a) - F(b).