
- •1.Механические гармонические колебания, их характеристики и простейшие колебательные системы.
- •2.Доказать возможность гармонических колебаний для физического маятника и определить все их характеристики и необходимые условия.
- •3. Электрические гармонические колебания в идеальном контуре, их свойства и характеристики.
- •4. Сложение гармонических колебаний параллельных и перпендикулярных направлений.
- •5. Затухающие механические и электрические колебания, основные характеристики и связь между ними.
- •6.Получить выражения для времени релаксации, логарифмического декремента затухания и добротности колебательной системы.
- •7.Вынужденные колебания, основные закономерности и характеристики.
- •8.Используя метод векторных диаграмм, получить выражения для амплитуды и фазы установившихся вынужденных колебаний.
- •9. Резонанс смещения и скорости смещения, основные закономерности и определяющие параметры.
- •10.Переменный электрический ток, квазистационарность, векторная диаграмма.
- •11.Получить выражение для добротности колебательного контура в случае вынужденных колебаний (переменного тока).
- •12 Автоколебания и основные их закономерности.
- •13. Параметрический резонанс и его основные закономерности.
- •14. Упругие волны в сплошной среде, основные свойства, закономерности и характеристики.
- •15. Волновое уравнение для упругих волн и его общее решение.
- •20. Волновой пакет. Дисперсия упругих волн.
- •21. Получить выражение для групповой скорости в случае простейшего волнового пакета и связи групповой скорости с фазовой.
- •22 . Дисперсия волн на глубокой воде; капиллярных волн.
- •23. Звуковые волны. Элементы акустики. Энергетическое воздействие ультразвука.
- •28. Получить в одномерном случае волновое уравнение для электромагнитных волн и выражение для фазовой скорости.
- •29. Эффект Доплера для электромагнитных волн. Продольный и поперечный эффекты.
- •30. Дипольное излучение, его характеристики и закономерности.
- •31. Когерентность света. Параметры когерентности. Оценки для типичных случаев.
- •32. Интерференция света. Параметры интерференции. Возможность наблюдения.
- •33. Рассчитать разность хода, координаты максимумов и минимумов, расстояние между интерференционными полосами и ширину полос в опыте Юнга.
- •35. Дифракция света. Метод зон Френеля. Критерий различных видов дифракции.
- •36. Дифракция Френеля. Простейшие дифракционные задачи.
- •37. Дифракция Фраунгофера. Дифракция на одной щели и на дифракционной решетке.
- •38. Вывести условия главных минимумов, главных максимумов, дополнительных минимумов и определить углы границ центрального максимума для дифракционной решетки.
- •39. Разрешающая способность оптических и спектральных приборов.
- •40. Рассчитать необходимый диаметр объектива оптической системы искусственного спутника для возможности фотографирования деталей заданных размеров.
- •41. Получить выражение для разрешающей способности дифракционной решетки как спектрального прибора.
- •42. Дифракция рентгеновских лучей на кристаллах. Рентгеновская спектроскопия и рентгеноструктурный анализ.
- •43. Основы голографии. Основные виды и механизм записи и воспроизведения изображения.
- •44.Поглощение и дисперсия света в веществе. Электронная теория.
- •46. Вывести условия, при которых происходит излучение Вавилова-Черенкова, и привести расчет соответствующего угла.
- •47.Поляризация света. Закон Малюса. Поляризаторы и анализаторы.
- •48.Поляризация света. Явление Брюстера. Стопа Столетова.
- •50.Двойное лучепреломление и его свойства.
- •51.Обосновать явление двойного лучепреломления с помощью свойств обыкновенного и необыкновенного лучей, используя принцип Гюгенса.
- •52.Искусственная оптическая анизотропия. Явление Керра.
- •53.Тепловое излучение, его свойства, характеристики и законы.
- •55.Формулы Рэлея-Джинса и Планка, связь и основания для их вывода.
- •56.С помощью формулы Планка вывести закон Стефана-Больцмана для теплового излучения.
- •57.С помощью формулы Планка вывести закон смещения Вина для теплового излучения.
- •59.Внешний фотоэффект, его вах, законы и механизм.
- •60.Уравнение Эйнштейна для фотоэффекта.
- •61.Давление света, его механизм и закономерности.
- •65.Опыт Резерфорда, планетарная модель атома и её недостатки (фатальные).
- •66.Модель Бора для водородоподобных атомов.
- •67.Вывести соотношения между различными видами энергии электрона для водородоподобного атома по теории Бора.
- •68.Получить выражения для радиуса отбиты и скорости электрона на ней для водородоподобного атома по теории Бора.
- •69.Рассчитать энергию ионизации, полную энергию электрона и получить сериальную формулу для спектра водородоподобного атома по теории Бора.
- •70.Корпускулярно-волновой дуализм свойств света, основные проявления, закономерности и интерпретация.
- •71.Рассчитать фазовую и групповую скорости волн де Бройля в классическом случае и в релятивистском случае.
- •72.Соотношения неопределенностей, виды, обоснования и интерпретация.
- •73.Волновая функция и основные, присущие ей закономерности. Уравнения Шредингера.
- •74.Свободная частица в квантовой механике, точное решение, параметры бегущих волн де Бройля.
- •75. Частица в одномерной потенциальной яме.
- •76.Получить решения уравнения Шредингера для частицы в одномерной потенциальной яме и выражение для энергии частицы. Сделать анализ полученных соотношений.
- •77.Получить выражение для энергии частицы в одномерной потенциальной ямы, описав её состояние как соответствующую стоячую волну.
- •79.Туннельный эффект.
- •81.Атом водорода в квантовой механике.
- •83.Принцип неразличимости тождественных частиц. Принцип Паули.
- •84.Периодическая система элементов, базовые положения и основные закономерности.
- •87.Вынужденное излучение и усиление света в веществе. Инверсное состояние вещества.
- •88.Оптические квантовые генераторы. Свойства лазерного излучения.
- •89.Строение и свойства атомного ядра. Основные характеристики.
- •90.Ядерные силы и их основные свойства. Энергия связи ядра и дефект массы.
- •92.Радиоактивность, основные закономерности и параметры.
- •93.Получить связь между постоянной радиоактивного распада, периодом полураспада и средним временем жизни радиоактивного ядра.
- •97.Ядерные реакции, их основные закономерности, характеристики и свойства.
- •98.Реакции деления атомного ядра, основные закономерности и применение.
- •100.Термоядерные реакции, их виды, механизм и оценка энергии.
- •104.Квантовая теория теплоемкости валентных электронов и газов.
- •105.Квантовая теория теплоемкости твердых тел. Фононы.
- •106.Зонная теория твердых тел. Отличие в строение металлов, диэлектриков и полупроводников.
- •107.Чистые и примесные полупроводники, их зонные структуры и основные свойства.
- •108.Доказать, что у чистых полупроводников уровень Ферми находится посредине запрещенной зоны.
- •109.Вывести формулу для зависимости удельной проводимости чистого полупроводника от температуры.
10.Переменный электрический ток, квазистационарность, векторная диаграмма.
Рассмотрим цепь переменного тока, содержащую последовательно включённые резистор, катушку и конденсатор (R,L,C) *схема1* *рисунок1*
Отсюда
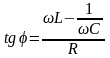 ;
;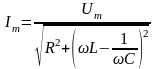 ;
;
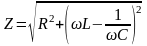
11.Получить выражение для добротности колебательного контура в случае вынужденных колебаний (переменного тока).
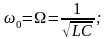
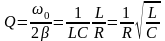
При
резонансе напряжений
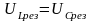 :
:
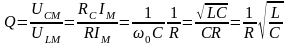 ;
;
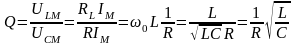
12 Автоколебания и основные их закономерности.
Огромный интерес для техники представляет возможность поддержания незатухающих колебаний. Если восполнять потери энергии реальной колебательной системы, то колебания станут незатухающими. Широко применяются автоколебания – незатухающие колебания в диссипативной системе за счёт постоянного внешнего источника энергии, причём свойства этих колебаний определяются самой системой. Автоколебательная система сама управляет внешним воздействием, обеспечивая согласованность поступления энергии определёнными порциями в нужный момент времени. Примером автоколебательной системы могут служить часы. Храповой механизм подталкивает маятник в такт с его колебаниями. Энергия, передаваемая при этом маятнику, берётся либо за счёт раскручивания пружины, либо за счёт опускающегося груза. Колебания воздуха в духовых инструментах и органных трубах также возникают вследствие автоколебаний, поддерживаемых воздушной струёй. Так же двигатели внутреннего сгорания, паровые турбины, ламповый генератор.
13. Параметрический резонанс и его основные закономерности.
Параметрический резонанс – увеличение амплитуды колебаний при периодическом изменении параметров тех элементов системы, в которых сосредотачивается энергия колебаний. Диаграмма параметрического резонанса в колеб. контуре: *диаграмма*
Мы
наблюдаем процесс накачки – изменение
параметров колебательной системы,
сопровождающееся положительной работай
внешних сил. Период накачки:
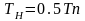
14. Упругие волны в сплошной среде, основные свойства, закономерности и характеристики.
Упругие волны – процесс распространения упругих колебаний в сплошной среде. Бывают продольными и поперечными. В продольных волнах частицы среды колеблются в направлении распространения волны. В поперечных – в плоскостях, перпендикулярных направлению распространения волны. Продольные волны могут распространяться в средах, в которых возникают упругие силы(деформации сжатия и растяжения), т.е. твёрдых, жидких и газообразных телах. Поперечные волны могут распространяться в среде в которой возникают упругие силы (при деформации сдвига), т.е. фактически только в твёрдых телах. Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими. Длина волны – расстояние между ближайшими частицами, колеблющимися в одинаковой фазе.
15. Волновое уравнение для упругих волн и его общее решение.
Общий
вид уравнения упругой волны: s=s(x,t).
Колебание точки лежащей в плоскости
«О», ч=0, описываются функцией s(0,t)=Acosωt.
«В» колеблется по тому же закону, но её
колебания будут отставать по времени
от колебаний источника на
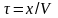
*рисунок*
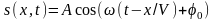 ;
Используем волновое число
;
Используем волновое число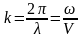 ;
;
Тогда
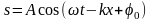 .
Предположим, что фаза постоянна:
.
Предположим, что фаза постоянна:
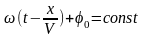 ;
;
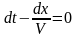 ;
;
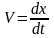 - скорость распространения волны в
уравнении – скорость перемещения фазы
волны – фазовая скорость,
- скорость распространения волны в
уравнении – скорость перемещения фазы
волны – фазовая скорость,
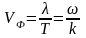 .
Вид уравнения при условии, что волна
распространяется в произвольном
направлении:
.
Вид уравнения при условии, что волна
распространяется в произвольном
направлении:
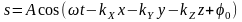 .
.
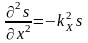 ;
;
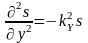 ;
;
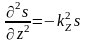 .
.
Тогда
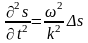 или
или
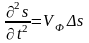 ,
т.к.
,
т.к.
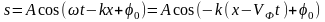 ,
то общее решение:
,
то общее решение:
 .
.
16. Получить волновое уравнение (дифференциальное уравнение волны) для плоских упругих продольных волн в твердом теле и выражение для фазовой скорости в этом случае.
Рассмотрим
деформацию тела:
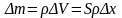 ;
;
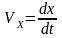 ;
;
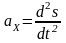 *рисунок*
*рисунок*
Деформация.
Связь напряжения σ и модуля Юнга Е:
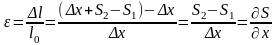
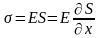 ;
;
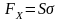 ;
;
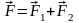 ;
;
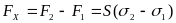 ;
;
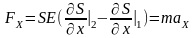 =>
=>
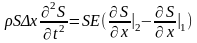 => Уравнение
=> Уравнение
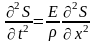 ;
;
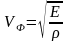 .
.
17. Перенос энергии упругими волнами, основные характеристики и связь между ними.
Величина,
характеризующая перенос энергии
упругими волнами Ф[Вт];
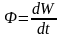 - поток энергии, dW-
энергия, проходящая через малый участок
поверхности, перпендикулярно ей. j
– плотность потока энергии.
- поток энергии, dW-
энергия, проходящая через малый участок
поверхности, перпендикулярно ей. j
– плотность потока энергии.
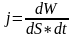 ;
[Вт/м*м] *рисунок*
;
[Вт/м*м] *рисунок*
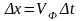 ;
;
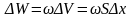 ;
;
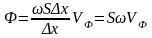 ;
;
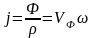
18. Рассчитать энергию и объемную плотность энергии для продольных упругих волн в твердом теле (для поперечных волн).
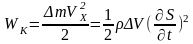 ;
;
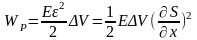 ;
;
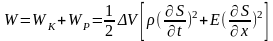 .
ω – объёмная плотность энергии.
.
ω – объёмная плотность энергии.
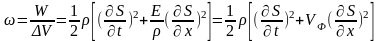 .
Пусть
.
Пусть
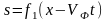 ,
,
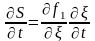 ;
;
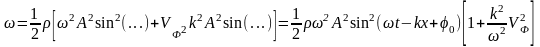 =>
=>
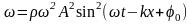 .
.
19 Стоячие упругие и электромагнитные волны. Узлы и пучности. Закономерности отражения волн.
Стоячие
волны – волны, образующиеся при наложении
двух бегущих синусоидальных волн,
распространяющихся навстречу друг
другу с одинак. частотами и амплитудами
(синфазные колебания точек пространства,
для которых амплитуда является
периодической функцией координаты).
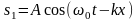 ;
;
 ;
;
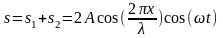 ,
т.к.
,
т.к.
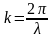 =>
=>
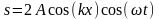 ;
;
*рисунок*
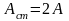 ;
;
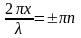 ,
т=0,1,2…
,
т=0,1,2… 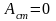 ;
;
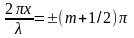 ,
ь=0,1,…
,
ь=0,1,…
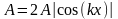 .
Пучности – точки, в которых амплитуда
стоячей волны, максимальна. Узлы –
точки, в которых амплитуда стоячей
волны, равна 0. В зависимости от того,
от какой среды происходит отражение,
уравнение стоячей волны имеет вид:
.
Пучности – точки, в которых амплитуда
стоячей волны, максимальна. Узлы –
точки, в которых амплитуда стоячей
волны, равна 0. В зависимости от того,
от какой среды происходит отражение,
уравнение стоячей волны имеет вид:
Образование узла связано с тем, что волна отражается от более плотной среды и меняет фазу на противоположную и у границы происходит сложение колебаний, в результате чего получается узел. Если же волна отражается от менее плотной среды, то изменения фазы не происходит и у границы складываются колебания с одинаковыми фазами – получается пучность.
