105.Квантовая теория теплоемкости твердых тел. Фононы.
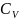(Твердого
тела) – 3R,
т.к. I
= 2*3 = 6;
Колебание одного атома приводит к колебанию других.
Фотон – квазичастица, сравнимая с упругой волной в твердом теле. Тепловое излучение твердого тела будем рассматривать как потом фононов, распространяющихся во всех направлениях. Следовательно каждый фотон обладает длиной волны (частотой) => энергией = hv
-
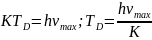температура Дебая;
Температура Дебая – температура, при которой характерная средняя энергия теплового движения в веществе равна энергии фонона с предельной частотой упругих колебаний кристаллической решетки.
103.Функция
f(E,T) называется функцией Ферми. Эта
функция определяется вероятностью
того, что квантовые состояния с энергией
Е заняты частицами при заданной
температуре Т. По её смыслу её не может
быть больше единицы.
Параметр
системы частиц EF, входящий в выражение
для функции Ферми, носит название
энергии Ферми (энергию Ферми называют
также химическим потенциалом), а
соответствующее значение по лекалу
энергий называется энергией
Ферми.
Формально,
исходя из (10), энергию Ферми можно
определить как энергию таких квантовых
состоянии, вероятность заполнения
которых частицами равна 0,5. Действительно,
из (10) следует, что f(EF,T) =0,5.
Энергия
Ферми квантовой системы фермионов
зависит от
концентрации
частиц n0 и от температуры Т, а значение
энергии Ферми при абсолютном нуле
температуры (здесь и далее абсолютный
нуль температуры понимается как предел
Т=>0, имеется в виду, что абсолютный
нуль недостижим) можно
рассматривать по формуле
. 
Обычно
рассматриваются системы, у которых 
.
Для таких систем cогласно (1) можно
пренебречь зависимостью энергии Ферми
от температуры и считать
Вид
функции Ферми приведен на рисунке.
полностью
заполненные частицами, а все квантовые
состояния с энергией -
пустые. Поэтому энергию Ферми при
абсолютном нуле
можно
определить как максимальную энергию
частиц данной системы при T=00K. За счет
нагрева системы часть частиц имевших
при T=00K энергии меньше уровня Ферми
приобретают энергии несколько выше
уровня Ферми. При этом область частично
заполненных квантовых состояний, т.е.
область, где,
,
имеет по шкале энергий размер порядка
2КТ.
106.Зонная теория твердых тел. Отличие в строение металлов, диэлектриков и полупроводников.
Зонная теория – раздел квантовой механики, рассматривающий движение электронов в тв. теле. Свободные электроны могут иметь любую энергию – их энергетический спектр непрерывен. Электроны, принадлежащие изолированным атомам, имеют определённые дискретные значения энергии. Но в тв. теле энергетический спектр электронов существенно иной, он состоит из отдельных разрешённых зон, разделённых зонами запрещённых энергий. Разрешённые энергетические зоны – области, в которых может находиться энергия электронов в тв. теле. Зонная теория тв. тела позволила с единой точки зрения истолковать существование металлов, диэлектриков и полупроводников, объясняя различие в их электрических св-вах. *рисунок*