1.Механические гармонические колебания, их характеристики и простейшие колебательные системы.
Колебаниями называется движение или процессы, которые характеризуются определённой повторяемостью во времени. Гармонические колебания – колебания, для которых колеблющаяся величина изменяется по закону sin или cos.
Уравнение гармонических колебаний s=A*cos(ω0t+φ)
А - амплитуда - максимальное значение колеблющейся величины.
ω0 - круговая (циклическая) частота.
φ – начальная фаза колебаний в момент t=0
Т – период – отношение времени колебаний к соответствующему числу полных колебаний.
ν – частота – число полных колебаний, совершаемых за единицу времени.
Дифференциальное уравнение гармонических колебаний:
Кинетическая энергия мат. точки (и потенциальная), совершающей прямолинейные гармонические колебания:
Т=
;
П=
Полная
энергия Е=Т+П=
;
Пример: качели + *рисунок*
2.Доказать возможность гармонических колебаний для физического маятника и определить все их характеристики и необходимые условия.
Для примера возьмём тв. тело, отклонённое от положения равновесия на угол α.
*рисунок*
При
малых углах: α<<
=> sinα≈α;
=> Уравнение примет вид
,
которое является дифф. уравн. гарм.
колебаний, где циклическая частота
ω0=
,
а период малых колебаний физ. маятника
;
,
где L=
-
приведённая длина.
3. Электрические гармонические колебания в идеальном контуре, их свойства и характеристики.
Электромагнитные колебания – колебания, при которых величины (заряды, токи, напряжения, электрические и магнитные поля) изменяются периодически. Для возбуждения и поддержания электромагнитных колебаний требуются определённые силы, простейшей из которых является колебательный контур – цепь, состоящая из подключённых последовательно катушки индуктивности L и конденсатора C ( может быть ещё резистор сопротивлением R).
*схема
контура*
.
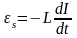По закону Кирхгофа: IR+
,
где
Тогда:
;
При сопротивлении в колебательном контуре R≈0; электромагнитные колебания в контуре являются гармоническими:
;
;
;
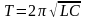4. Сложение гармонических колебаний параллельных и перпендикулярных направлений.
Для сложения гармонических колебаний одного направления и одинаковой частоты воспользуемся методом вращающегося вектора амплитуды.
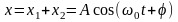
Рассмотрим результат сложения двух гармонических колебаний с одинаковыми частотами ω, происходящих во взаимно перпендикулярных направлениях вдоль осей х и у.
,
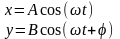где А и В – амплитуды, для простоты
обозначения разность фаз =φ.
Уравнение
траектории результирующего колебания
находится путём исключения из выражения
t:
при φ=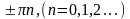
;
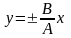при
φ=
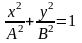
Широко используемый метод исследования соотношений частот и разности фаз складываемых колебаний – анализ фигур Лиссажу.