Зоммерфельда теория

ЗОММЕРФЕЛЬДА ТЕОРИЯ МЕТАЛЛОВ - предложена А. Зоммерфельдом (A. Sommerfeld) в 1928. 3. т. м. представляет собой дальнейшее развитие Друде теории металлов, отличаясь от последней тем, что распределение свободных электронов по энергиям описывается Ферми - Дирака распределением, а не Больцмана распределением .Как и теория Друде - Лоренца, 3. т. м. пренебрегает взаимодействием электронов друг с другом, а их взаимодействие с кристаллич. решёткой сводит лишь к соударениям, при к-рых импульс электрона меняется скачком. 3. т. м. позволила объяснить отсутствие заметного вклада электронного газа в теплоёмкость металла при комнатной темп-ре. В 3. т. м. этот вклад равен:  C_v=(p²/2).(kT/E_F).nk,  где E_F - Ферми энергия, Т - абс. темп-pa, п - концентрация свободных электронов. При комнатной темп-ре эта теплоёмкость ~ в 100 раз меньше значения 3 nk/2, даваемого теорией Друде (при низких темп-рах электронный вклад в C_v может оказаться сравнимым с решёточным, обычно это происходит при темп-ре в неск. К). Др. класс явлений, где теории Друде и Зоммерфельда приводят к разл. результатам, - кинетич. эффекты, обусловленные наличием разброса электронов по энергиям (магнетосопротивление, электроннаятеплопроводность, термомагн. явления, термоэлектрич. явления). 3. т. м. даёт для этих эффектов величину, в (E_F/kT)ⁿ (n=1, 2) раз меньшую, чем в теории Друде, что согласуется с экспериментом. 3. т. м. не могла объяснить эффекты, обусловленные зонной структурой энергетич. спектра металлов, напр., положит. знак постоянной Холла у мн. проводников (см. Холла эффект ),и сложной формой ферми-поверхности. Тем не менее во мн. случаях 3. т. м. в силу своей простоты оказывается удобной для численных оценок и качеств. объяснения электронных свойств металлов.

15.Первое правило

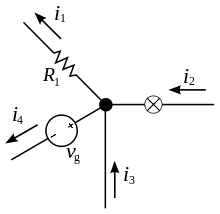
Сколько тока втекает в узел, столько из него и вытекает. i₂ + i₃ = i₁ + i₄

Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:

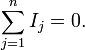Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда. Второе правило Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений 

для переменных напряжений  Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее). Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

ПРИМЕР

Количество узлов: 3.  Количество ветвей (в замкнутых контурах): 4. Количество ветвей, содержащих источник тока: 0.  Количество контуров: 2. Для приведённой на рисунке цепи, в соответствии с первым правилом, выполняются следующие соотношения:

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, здесь токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными. Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов. В соответствии со вторым правилом, справедливы соотношения:

Полученная система уравнений полностью описывает анализируемую цепь, и её решение определяет все токи и все напряжения ветвей, такой подход к анализу цепи принято называть методом узловых потенциалов.