14. Реальные газы и жидкости .

Изотермы реального газа. Уравнение Ван-дер-Ваальса. Поверхностное натяжение. Давление Лапласа. Капиллярные явления. Осмос.

Для реальных газов необходимо учитывать размеры мо­лекул и их взаимодействие друг с другом, поэтому модель идеального газа и уравнение Клапейрона—Менделеева.

(для моля газа), описывающее иде­альный газ, для реальных газов непри­годны.

1. Учет собственного объема молекул.

не , a , где b — объем, занимаемый самими молекулами. Объем b равен учетверенному соб­ственному объему молекул.

2. Учет притяжения молекул.

Приводит к появле­нию дополнительного давления на газ, называемого внутренним давлением.

Вводя эти поправки, получим уравне­ние Ван-дер-Ваальса для моля газа (урав­нение состояния реальных газов):

где поправки а и b — постоянные для каж­дого газа величины, определяемые опыт­ным путем (записываются уравнения Ван-дер-Ваальса для двух известных из опыта состояний газа и решаются относительно а и b).

Изотермы Ван-дер-Ваальса и их анализ

Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ва­альса — кривые зависимости р от V_m при заданных Т, определяемые уравнением Ван-дер-Ваальса для моля газа.

Для нахождения критических пара­метров напишем (1)

По­скольку в критической точке все три корня совпадают и равны V_к, уравнение приво­дится к виду

Или (2)

Так как уравнения (1) и (2) тожде­ственны, то в них должны быть равны и коэффициенты при неизвестных соответ­ствующих степеней. Поэтому можно за­писать

Решая полученные уравнения, найдем:

Если через крайние точки горизонталь­ных участков семейства изотерм провести линию, то получится колоколообразная кривая (рис. 91), ограничивающая об­ласть двухфазных состояний вещества. Эта кривая и критическая изотерма делят

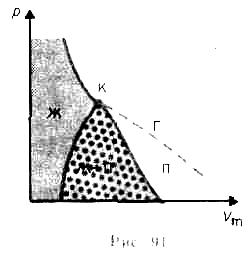
Сравнивая изотерму Ван-дер-Ваальса с изотермой Эндрюса (верхняя кривая на рис. 92), видим, что последняя имеет пря­молинейный участок 2—6, соответствую­щий двухфазным состояниям вещества. Правда, при некоторых условиях могут быть реализованы состояния, изображае­мые участками ван-дер-ваальсовой изо­термы 5—6 и 2—3. Эти неустойчивые со­стояния называются метастабильными. Участок 2—3 изображает перегретую жидкость, 5—6 — пересыщенный пар. Обе фазы ограниченно устойчивы

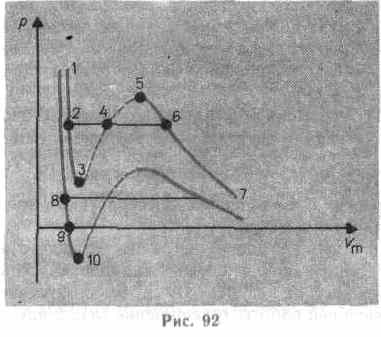
Вещество под отрицательным давлением находится в со­стоянии растяжения. При некоторых усло­виях такие состояния также реализуются. Участок 8—9 на нижней изотерме соответ­ствует перегретой жидкости, участок 9— 10 — растянутой жидкости.

Поверхностное натяжение

Поверхностное натяжение а равно силе поверхностного натяжения, приходя­щейся на единицу длины контура, ограни­чивающего поверхность. Единица повер­хностного натяжения — ньютон на метр (Н/м) или джоуль на квадратный метр (Дж/м²) Большин­ство жидкостей при температуре 300 К имеет поверхностное натяжение по­рядка 10^-2—10^-1 Н/м. Поверхностное на­тяжение с повышением температуры уменьшается, так как увеличиваются средние расстояния между молекулами жидкости.

Из практики известно, что капля воды растекается на стекле и принимает форму, изображенную на рис. 98, в то время как ртуть на той же поверхности превращает­ся в несколько сплюснутую каплю (рис. 99). В первом случае говорят, что жидкость смачивает твердую поверхность, во втором — не смачивает ее. Смачивание зависит от характера сил, действующих между молекулами поверхностных слоев соприкасающихся сред.

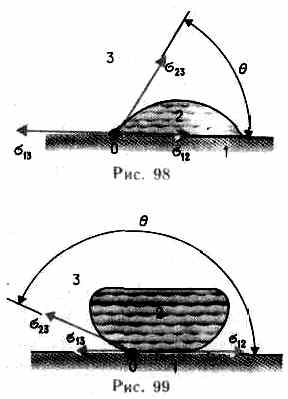
Пол­ное смачивание (в данном случае =0). Если ₁₂>₁₃+₂₃, то жидкость стягива­ется в шаровую каплю, в пределе имея с ней лишь одну точку соприкосновения (например, капля воды на поверхности парафина),— имеет место полное несма­чивание (в данном случае =).

.

Давление под искривленной поверхностью жидкости

На каждый бес­конечно малый элемент длины l этого контура действует сила поверхностного натяжения F=l, касательная к по­верхности сферы. Разложив F на два компонента (F₁ и F₂), видим, что гео­метрическая сумма сил F₂ равна нулю. Поэтому равнодействующая сил поверхно­стного натяжения, действующих на вы­резанный сегмент, направлена перпенди­кулярно плоскости сечения внутрь жидко-

сти и равна алгебраической сумме со­ставляющих F₁:

Разделив эту силу на площадь основания сегмента r², вычислим избыточное (до­бавочное) давление на жидкость:

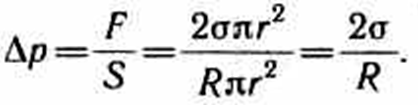
Формула Лапласа,

Капиллярные явления

Если поместить узкую трубку (капилляр) одним концом в жидкость, налитую в ши­рокий сосуд, то вследствие смачивания или несмачивания жидкостью стенок ка­пилляра кривизна поверхности жидкости в капилляре становится значительной.

где  — плотность жидкости, g — ускоре­ние свободного падения.

Если m — радиус капилляра,  — крае­вой угол, то из рис. 101 следует, что , откуда

В соответствии с тем, что смачиваю­щая жидкость по капилляру поднимается, а несмачивающая — опускается,

В тонких капиллярах жидкость под­нимается достаточно высоко. Так, при полном смачивании ( = 0) вода (=1000 кг/м³, =0,073 Н/м) в капилляре диаметром 10 мкм поднимается на высоту h3 м.

Капиллярные явления играют боль­шую роль в природе и технике. Например, влагообмен в почве и в растениях осуще­ствляется за счет поднятия воды по тон­чайшим капиллярам. На капиллярности основано действие фитилей, впитывание влаги бетоном и т. д.