1) По Кельвину: невозможен круговой процесс, единственным результатом кото­рого является превращение теплоты, полу­ченной от нагревателя, в эквивалентную ей работу;

2) По Клаузиусу: невозможен круговой процесс, единственным результатом кото­рого является передача теплоты от менее нагретого тела к более нагретому.

Первые два начала термодинамики да­ют недостаточно сведений о поведении термодинамических систем при нуле Кель­вина. Они дополняются третьим началом термодинамики, или теоремой Нернста — Планка: энтропия всех тел в со­стоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина:

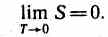
Цикл Карно и его к. п. д. для идеального газа

Из формулировки второго начала термо­динамики по Кельвину следует, что вечный двигатель второго рода — периодически действующий двигатель, совершающий работу за счет охлаждения одного источ­ника теплоты,— невозможен.

Основываясь на втором начале термо­динамики, Карно вывел теорему, носящую теперь его имя: из всех периодически дей­ствующих тепловых машин, имеющих оди­наковые температуры нагревателей (T₁) и холодильников (Т₂), наибольшим к. п. д. обладают обратимые машины;

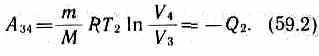
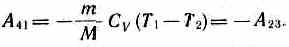
Работа, совершаемая в результате кругового процесса,

А=А₁₂ + А₂₃ + A₃₄ + A₄₁= Q₁+A₂₃ -Q₂ -A₂₃=Q₁-Q₂

=A/Q₁=(Q₁-Q₂)/Q₁.

Применив уравнение для адиабат получим

откуда

V₂/V₁ = V₃/V₄.

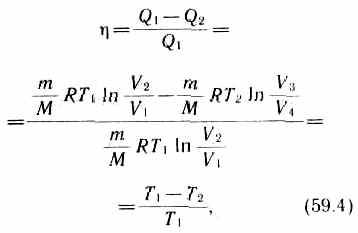13.

Явление переноса.

Законы диффузии, теплопроводности и внутреннего трения (вязкости) и их обоснование в молекулярно-кинетической теории. Движение жидкости (газа) по трубам. Формула Пуазейля.

Диффузия, теплопроводность и внутреннее трение.

Выведем основное уравнение явления переноса:

 - переносимый параметр

x = 2<>

<> – средняя длина свободного пробега молекул.

- основное уравнение явления переноса.

1. Диффузия

 = m;

- уравнение диффузии (уравнение Фика).

- градиент плотности.

2. Теплопроводность

; (i – степень свободы, i= 3, 5 ,6)

- уравнение теплопроводности (уравнение Фурье).

-

3. Внутреннее трение

 = p = mV

=

- уравнение трения (уравнение Ньютона).

P = F·t

Движение жидкости (газа) по трубам. Формула Пуазейля.

Существует два режима течения жид­костей. Течение называется ламинарным (слоистым), если вдоль потока каждый выделенный тонкий слой скользит относи­тельно соседних, не перемешиваясь с ни­ми, и турбулентным (вихревым), если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа).

Рейнольдс установил, что ха­рактер течения зависит от безразмерной величины, называемой числом Рейнольдса: где — кинематическая вязкость;

 — плотность жидкости; (v)—средняя по сечению трубы скорость жидкости; d — характерный линейный размер, например диаметр трубы. При малых значениях числа Рейнольдса (Re1000) наблюдается ламинарное течение, переход от ламинарного течения к турбулентному происходит в области 1000:Re2000, а при Re = 2300 (для гладких труб) течение — турбулентное. Если число Рейнольдса одинаково, то ре­жим течения различных жидкостей (га­зов) в трубах разных сечений одинаков.

Методы определения вязкости

1. Метод Стокса. Этот метод определе­ния вязкости основан на измерении скоро­сти медленно движущихся в жидкости не­больших тел сферической формы.

Измерив скорость равномерного движения шарика, можно определить вязкость жид­кости (газа).

2. Метод Пуазейля. Этот метод осно­ван на ламинарном течении жидкости в тонком капилляре. Рассмотрим капилляр радиусом R и длиной l. В жидкости мыс­ленно выделим цилиндрический слой ради­усом r и толщиной dr (рис. 54). Сила внут­реннего трения, действующая на боковую поверхность этого слоя,

где dS — боковая поверхность цилиндри­ческого слоя; знак минус означает, что при возрастании радиуса скорость уменьша­ется.

Для установившегося течения жидко­сти сила внутреннего трения, действую­щая на боковую поверхность цилиндра, уравновешивается силой давления, дей­ствующей на его основание:

После интегрирования, полагая, что у стенок имеет место прилипание жидкости, т. е. скорость на расстоянии R от оси равна нулю, получим

Отсюда видно, что скорости частиц жид­кости распределяются по параболиче­скому закону, причем вершина параболы лежит на оси трубы. За время t из трубы вытечет жидкость, объем которой

откуда вязкость