9. 9.Основы молекулярно-кинетической теории.

Основные положения молекулярно-кинетической теории. Идеальный газ. Термодинамические параметры. Равновесные и неравновесные процессы. Уравнение состояния. Основное уравнение молекулярно-кинетической теории идеального газа.

В молекулярно-кинетической теории пользуются идеализированной моделью идеального газа, согласно которой считают, что:

1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;

2) между молекулами газа отсутствуют силы взаимодействия;

3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

Модель идеального газа можно использовать при изучении реальных газов, так как они в условиях, близких к нормальным (например, кислород и гелий), а также при низких давления» и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки, учитывающие собственный объем молекул газа и действующие молекулярные силы, можно перейти к теории реальных газов.

Идеальный газ. Термодинамические параметры. Уравнение состояния. Основное уравнение мкт.

Вывод основного уравнения молекулярно-кинетической теории (МКТ) идеального газа.

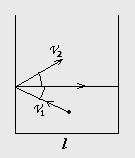Рассмотрим сосуд кубической формы с размером l:

Пусть в этом объеме движется только один атом и сталкивается об стенку сосуда со скоростью V₁ и отражается V₂ .

Определим силу удара об стенку сосуда (по II закону Ньютона):

f ·t = m ·V

V = 2V; V = V₂ – V₁

 ; – сила удара одной молекулы об стенку сосуда

Вычислим силу удара об стенку сосуда N – молекул:

– средняя квадратичная скорость.

9. Классическая статистика.

Закон равномерного распределения энергии по степеням свободы. Длина свободного пробега и эффективный диаметр молекул. Распределение Максвелла. Барометрическая формула. Распределение Больцмана.

Классическая статистика. Функция распределения Максвелла. Барометрическая формула. Распределение Больцмана.

Закон равномерного распределения энергии по степеням свободы молекул.

В классической статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень «обладает» вдвое большей энергией потому, что на нее прихо­дится не только кинетическая энергия (как в случае поступательного и вращательного движений), но и потенциальная, причем средние значения кинетической и потенциаль­ной энергий одинаковы. Таким образом, средняя энергия молекулы

где i — сумма числа поступательных, числа вращательных в удвоенного числа колеба­тельных степеней свободы молекулы:

Внутренняя энергия для произвольной массы т газа.

где М — молярная масса,  — количество вещества.

Средняя длина свободного пробега молекул и эффективный диаметр молекулы.

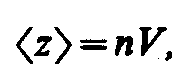
Классическое распределение по скоростям (Максвелла):

Справедливо для всех частиц:

dN – число частиц, попадающих в определенный интервал скоростей.

N – число всех частиц.

f(V) – функция распределения по скоростям

dV – элементарный объем скоростей.

Рассмотрим функцию распределения по скоростям в сферической системе координат:

- функция распределения Максвелла.

Величина А (амплитуда вероятности) находится из условия нормировки:

- условие нормировки

;

Аналогично находим (v_y) и (v_z):

тогда

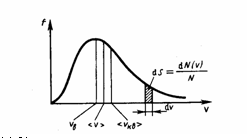
Барометрическая формула. Распределение Больцмана.

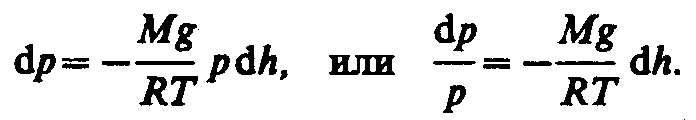
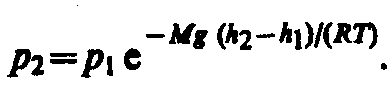
11 Первое закон термодинамики.

Внутренняя энергия системы. Теплоемкость вещества. Первый закон термодинамики. Применение первого закона термодинамики к изопроцессам в идеальном газе. Адиабатический процесс.

Внутренняя энергия газа