8.Алгебра логики. Основные понятия и тождества

Логические сообщения – это сообщения истинность и ложность которых может быть оценена однозначно. Каждое логическое сообщение может быть заменено математическим эквивалентом, т.е. логической функцией. Логические функции в отличие от аналоговых принимают лишь два значения 0 (в случае ложности) и 1 (в случае истинности). логические операции:

1) «НЕ» – логические отрицание или инверсия

2) «ИЛИ» – сложение или дизъюнкция (). Операцию «ИЛИ» можно выполнять для 2^х, 3^х и более переменных. Выходная функция равна 1, если хотя бы одна из независимых входных переменных равна 1.

3) «И» – логическое умножение или конъюнкция.().

4) Сложение (сумма) по модулю 2 (Исключающее (логическое)_или)

5) стрелка пирса (или-не)(↓)

6) штрих шеффера ( и-не)(∕)

Справедливы законы:

1)переместительный a+b=b+a; a*b=b*a

2) сочетательный а+(в+с)=(а+в)+с; а*(в*с)=(а*в)*с

3)распределительный а*(в+с)=а*в+а*с; а+(в*с)=(а+в)*(а+с)

4)Закон поглощения: а(а+в)=а; а+ав=а; а(а+в)(а+с)=а; а+ав+ас=а.

5)Закон склеивания: ;

Для осуществления операций над логическими выражениями пользуются рядом тождеств:

1) А+А=А; 2) ; 3) А+0=А; 4) А+1=1; 5) АА=А; 6) ; 7) А0=0; 8) А1=А; 9) ; 10) ;

Теорема Де Моргана

; (идет разрыв и меняем знак).

Число переменных м.б. различным.

Используя данные тождества можно упростить логические уравнения и свести к минимуму число логических элементов необходимых для реализации логич функции.

Совокупность элементарных функций с помощью которых можно записать логическую функцию более сложного вида называется базисом.

Синтез логич схем в базисе И-НЕ

Синтез логич схем в базисе ИЛИ-НЕ

9. Минимизация логических функций. Общие сведения. Диаграммы вейча

Упрощение логических функций с помощью тождеств представляет трудности особенно при большем числе вх переменных.

В этом случае приминяются методы минимизации:

1)диагр-мы Вейча,

2)Карты карно - предусматривает задание ФАЛ в виде координатных карт состояний. После записи ФАЛ в карту Карно сразу можно записать минимальную форму функции, что существенно уменьшает вероятность появления ошибки,

3)метод Квайна-Мак-Класки использование метода для функций с большим количеством аргументов и значительно уменьшает вероятность появления ошибки,

4)мет.неопред.коэфф

Метод диаграмм Вейча

Данный метод используется в основном для 2^х, 3^х, 4^х 5^ти переменных. Рассмотрим случай 4^х переменных. В данном случае диаграмма состоит из 16^ти возможных комбинаций вх переменных. На каждой клетке диаграммы обозначены значения каждой из 4^х переменных. Рассмотрим этапы минимизации по диаграмме Вейча:

1.Задается некоторое логическое уравнение, которое необходимо преобразовать (исключить общие знаки инверсии, применить закон де Моргана, повторения, поглощения и склеивания) Привести к виду СДНФ, СКНФ

2.Заполнить диаграмму Вейча, если в данном выражении есть соответствующие комбинации вх переменных, то клетки диаграммы обозначаются единицей

3.Проводится склейка клеток, т.е. можно объединить целую заполненную строку, целый столбец, полстроки, полстолбца. Можно склеивать соседние строки, столбцы, полустроки, полустолбцы. Можно объединять нижний, верхний, правый и левый края. Нельзя соединить нечетное число клеток клетки по диагонали.

4.Расшифровка склеек. Каждая склейка в результате должна быть представлена в виде конъюнкции переменных. В результате расшифровок склеек получаем результат минимизации, т.е. новое упрощенное логическое выражение.

5. Строится новая логическая схема, в выбранном базисе.

ПРИМЕР

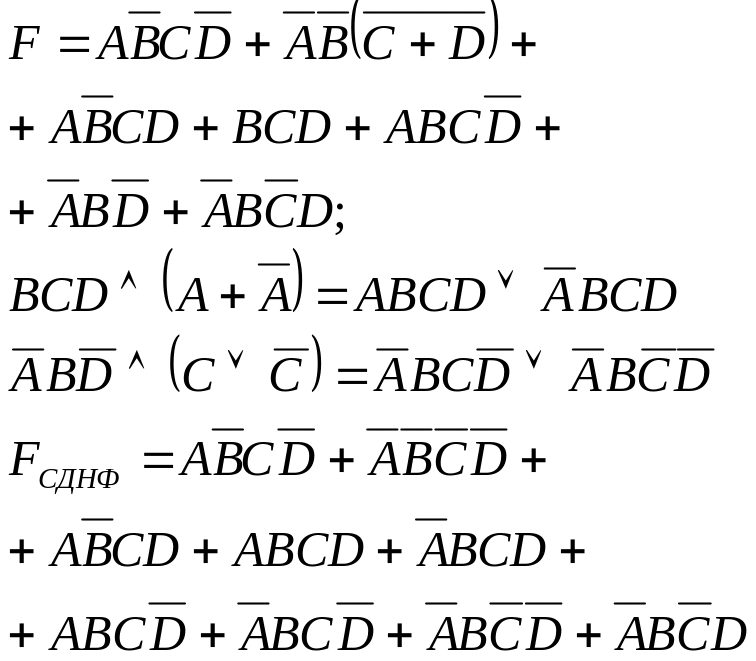
заполняем клетки диаг-мы Вейча:

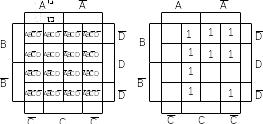
Склейка:

Результат минимизации

Строим лог схему: