
- •Раздел 20. Теория линии передач конечной длины.
- •20.1. Распространение электромагнитной волны в линиях передач конечной длины.
- •20.2. Коэффициент отражения. Коэффициент бегущей волны (кбв). Коэффициент стоячей волны (ксв).
- •20.3. Аналогия между произвольной линией передачи и длиной линии.
- •20.4. Нормированное эквивалентное сопротивление лп.
- •20.5. Волновое сопротивление линии передач по напряжению и току.
20.5. Волновое сопротивление линии передач по напряжению и току.
В курсе ОТЦ было известно волновом сопротивлении. Речь идет о произвольных ЛП. Введение волнового сопротивления волны типа Т не встречает трудности, т.к. электромагнитное поле имеет вихревой характер, поэтому понятие напряжение и ток не могут быть введены однозначно. Так контурный интеграл от напряженности электрического поля зависит не только от начальной и конечной точек интегрирования, но и от формы контура.
Аналогично
контурный интеграл от напряжения
магнитного поля так же зависит от формы
контура. В этом случае чтобы устранить
эту трудность обычно заранее оговариваривают
используемую форму контура. Подробнее
процедуру определения волнового
сопротивления рассмотрим на примере
волны
![]() в прямоугольном волноводе. Предельные
токи, текущие в противоположном
направлении по широким стенкам волновода,
в этом случае рассматриваются как токи
эквивалентные току длинной линии.
в прямоугольном волноводе. Предельные
токи, текущие в противоположном
направлении по широким стенкам волновода,
в этом случае рассматриваются как токи
эквивалентные току длинной линии.
![]()
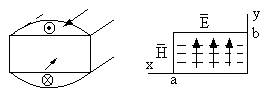
![]()
![]()
![]()
![]()
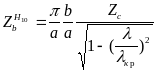
 ,где
,где
![]()
![]()
Контуры интегрирования можно и иначе при этом мы получим другое выражение для волнового сопротивления. При любых вариантах
![]() 1
1
где А -это величина, зависящая от формы контура.
При вычислении коэффициента отражения в аналитическое выражение входит отношение волновых сопротивлений, поэтому при подобных расчетах не имеет принципиального значения выбора формы контура. Соотношение (1) широко используется в технике СВЧ для приближенного определения К.О. от стыка двух прямоугольных волноводов с разными размерами a и b.
![]()
20.6. Круговая диаграмма полных сопротивлений.
![]()
для построения диаграммы этого соотношения перепишем (1)
![]() где
Р1-jP2=-P
где
Р1-jP2=-P
Выделим в соотношении (2) Re и Im части
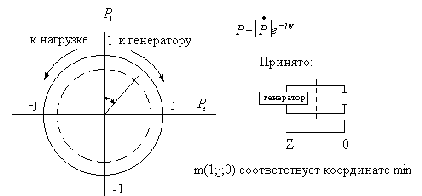
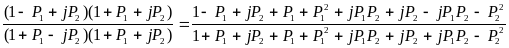
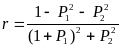 3
3
![]() 4
4
Путем несложных преобразований из соотношений (3,4) можно получить следующие выражения
![]() 5
5
Если
(5), (6) рассматривать как уравнение кривых
в системе координат Р1;
P2
то из (5),(6) следует, что эти уравнения
являются уравнениями окружности.
Соотношение (5) соответствует окружности
с радиусом
![]() с центром в.
с центром в.![]()
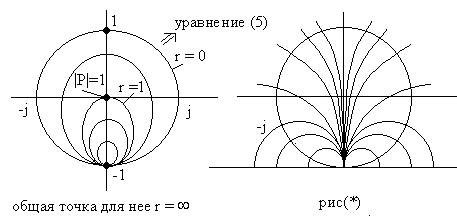
Из
(6) следует, что это окружность с радиусом
![]() и центром
и центром
![]() .
Реактивное
сопротивление имеющее индуктивный
характер соответствуют окружности
расположенной справа от оси (см. рис. *)
.
Реактивное
сопротивление имеющее индуктивный
характер соответствуют окружности
расположенной справа от оси (см. рис. *)
Реактивное сопротивление, имеющее емкостной характер соответствуют окружности расположенной слева..Для пассивных цепей модуль коэффициента отражения З меньше или равен 1 и все решения уравнения укладываются внутри круга Р=1
поэтому все решения вне круга Р=1 следует отбросить как не имеющие смысла для пассивных цепей. Совместим кривые изображений на этих рисунков на одной монограмме
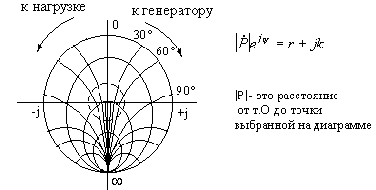
![]() На
внешней окружности круговой диаграммы
нанесены значения
На
внешней окружности круговой диаграммы
нанесены значения
![]() подставляя
значения
подставляя
значения
![]()
 Положительным
значениям Z-Zn
соответствуют перемещениям от нагрузки
к генератору. Полному повороту вектора
Положительным
значениям Z-Zn
соответствуют перемещениям от нагрузки
к генератору. Полному повороту вектора
![]() соответствует изменение угла
на .
соответствует изменение угла
на .
![]()
![]()
Круговая диаграмма полных сопротивлений одновременно является круговой диаграммой полных проводимостей
ZZn(min)
![]()
![]()
![]()
![]()
соответствует круговая диаграмма полных сопротивлений. Эту же круговую диаграмму можно использовать как круговую диаграмму проводимостей. В случае круговой диаграммы сопротивления отсчет физической проводимости относительно min эл. поля. При этом термин сопротивления необходимо заменить проводимостью.
Из
сравнений формул:![]()
![]()
Следует, что переход от сопротивлений к проводимостям соответствует повороту на круговой диаграмме на 180
Т.о. на диаграмме полных сопротивлений точки соответс.
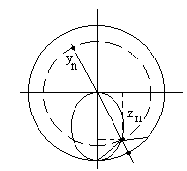
![]() лежат на противоположных концах
диаметра окружности (радиус которой
равен модулю коэффициента отражения)
с центром в начале координат.
лежат на противоположных концах
диаметра окружности (радиус которой
равен модулю коэффициента отражения)
с центром в начале координат.
