
- •Раздел 20. Теория линии передач конечной длины.
- •20.1. Распространение электромагнитной волны в линиях передач конечной длины.
- •20.2. Коэффициент отражения. Коэффициент бегущей волны (кбв). Коэффициент стоячей волны (ксв).
- •20.3. Аналогия между произвольной линией передачи и длиной линии.
- •20.4. Нормированное эквивалентное сопротивление лп.
- •20.5. Волновое сопротивление линии передач по напряжению и току.
Раздел 20. Теория линии передач конечной длины.
20.1. Распространение электромагнитной волны в линиях передач конечной длины.
Реальные линии передачи всегда имеют конечную длину. Включение в некоторое сечение нагрузки приводит к изменению граничных условий, как в данном сечении, так и во всей линии. Обычно это изменение структуры представляют как результат интерференции падающих и отраженных волн в линии передач.
Подробнее рассмотрим свойство отраженной волны:
1) в предыдущем параграфе мы отмечали, что в общем случае в ЛП может распространяться бесконечное число типов волн, которые в частности отличается структурой типов поперечной плоскости.
2) Очевидно, что сколько угодно сложную отраженную волну можно представить, как суперпозицию вот этого бесконечного числа волн.
3) Однако, при правильно выбранных размерах обеспечивается одномодовый режим на достаточном удалении от нагрузки. Отраженная волна так же относится к основному типу (на расстоянии нескольких длин волн от нагрузки высшие типы практически будут отсутствовать). Т.е. на расстоянии нескольких длин волн отраженная волна характеризуется такой же поперечной структуры, как и волна падающая.
Если в месте включения нагрузки структура поля такова, что в ней отсутствует волна низшего типа, то на достаточном удалении от нагрузки она будет отражаться в соответствии с законом сохранения энергии. В этом случае полагается, что падающая волна полностью поглощается в нагрузке и этот режим называется согласованным или режимом бегущей волны.
20.2. Коэффициент отражения. Коэффициент бегущей волны (кбв). Коэффициент стоячей волны (ксв).
Т.к. в одномодовой линии передачи подающая и отраженная волны имеют одинаковую структуру можно записать следующим соотношением
![]() 1
1
,где
![]() это
коэффициент отражения электрического
поля, зависящий от одной координаты
(Z).
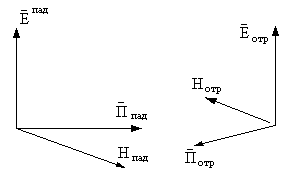
Полагая, в соответствии с рисунком, что
падающие и отраженные волны имеют
нулевое значение фазы при Z=0.
это
коэффициент отражения электрического
поля, зависящий от одной координаты
(Z).
Полагая, в соответствии с рисунком, что
падающие и отраженные волны имеют
нулевое значение фазы при Z=0.
![]() 2
2
![]() 3
3
![]() Подставляя
(2) и (3) в (1) получим
Подставляя
(2) и (3) в (1) получим
![]()
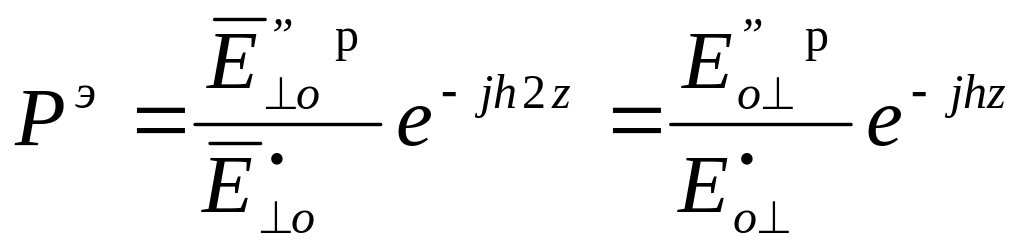
![]()
г де
Рн
-это
коэффициент отражения в сечении,
где включена нагрузка (Z=0).
де
Рн
-это
коэффициент отражения в сечении,
где включена нагрузка (Z=0).
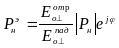
![]()
![]() -
коэффициент отражения магнитного поля.
-
коэффициент отражения магнитного поля.
![]()
![]() -
характеристическое сопротивление
соответствующего типа волны.
-
характеристическое сопротивление
соответствующего типа волны.
![]()
![]()
В дальнейшем будем пользоваться коэффициентом отражения только по электрическому полю. В произвольном сечении ЛП конечной длины результирующее поле представляет собой суперпозицию подающей и отраженной волн.
![]() 6
6
![]() 7
7
![]() 8
8
![]() 9
9
![]()
![]()
![]() 10
10
9
(10,11) пронормируем относительно Епад
![]() 12
12
![]() 13
13
![]()
Из
(12) следует, что min
значение нормиров. напряжен. Есть
![]()
Cos (2hzn - ) = -1 2hz=(2n -1)+ 14
n коорд. min
к
 оордината
max
оордината
max
![]() определяется cos.
(2hzn
- )
= 1
определяется cos.
(2hzn
- )
= 1
![]() 15
15
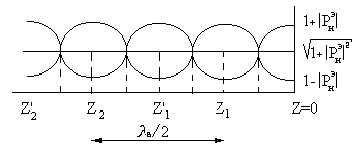
от координаты Z=0.Расстояние
между соседним min или max
равно
![]() .
.
Из соотношения(14) можно
определить фазу коэффициента
отражения от нагрузки, если
координата
min
![]() (например, из экспериментальных
измерений).
(например, из экспериментальных
измерений).
 =
=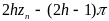 16
16


Аналогичным образом фаза нагрузки может (17) быть определена по max.
=
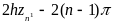
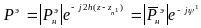 18
18
Отношение min напряж. или магнитного поля к max называется коэффициентом бегущей волны.

![]() 19
19
![]() 20
20
Наряду с коэффициентом отражения эти два коэффициента также характеризуют режим распространения волны в линии передач конечной длины.
В том случае, когда коэффициент отражения от нагрузки =0
![]()
![]()
![]() при
при
![]()
![]()
![]()
