6.3. Метод трапеций

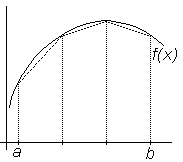
В этом методе подынтегральная функция f(x) на интервале [x_i,x_i+1] заменяется полиномом первой степени, т.е. наклонной прямой линией. Обычно эта прямая проводится через значения  f(x) на границах интервала (рис.6.6). В этом случае приближенное значение частичного интеграла определяется площадью трапеции:

Рис.6.6. Геометрическая интерпретация метода трапеций

, т.е. , а численное значение интеграла на всем [a,b] . Это вычислительная формула метода трапеций.

(6.12) (6.13)

Блок-схему алгоритма метода трапеций предлагается студентам разработать самим.

Оценим погрешность  R_i. Для этого разложим функцию  f(x) в ряд Тейлора около точки x_i :

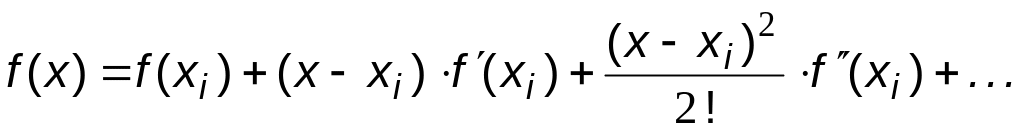
(6.14)

Тогда

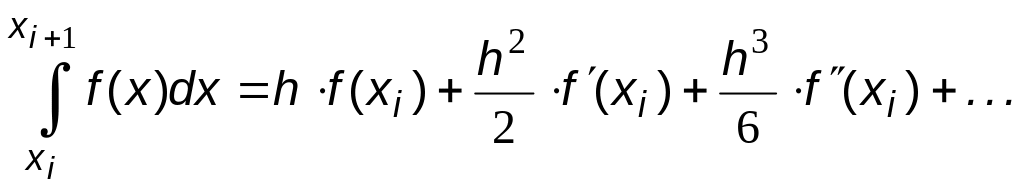
(6.15)

С помощью разложения (6.14) вычислим подынтегральную функцию в точке  x_i+h :

откуда

(6.16)

Подставляя произведение (6.16) в выражение (6.15), получим

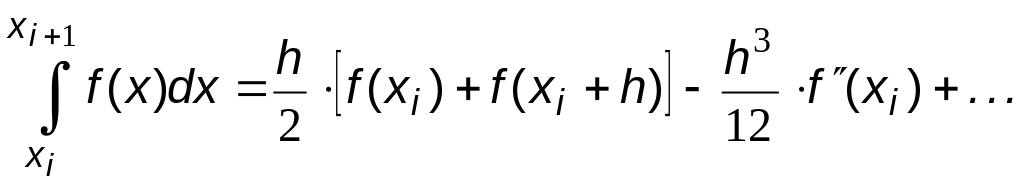
(6.17)

Сравнивая (6.12) и (6.17), получаем выражение для главного члена погрешности частичного интеграла

.

Тогда главный член полной погрешности метода трапеций имеет вид

,

(6.18)

т.е. метод трапеций имеет также второй порядок, но его погрешность в два раза больше, чем в методе средних прямоугольников, поэтому, если подынтегральная функция задана аналитически, то предпочтительнее из методов второго порядка использовать метод средних прямоугольников.

6.4. Экстраполяционный переход к пределу

Формулу (6.18) для погрешности метода трапеций можно записать в виде

,

где С - величина, не зависящая от шага разбиения h.

Для уточнения метода трапеций можно применить следующую манипуляцию: вычисляются два значения  S_h и S_k одного и того же интеграла для разных разбиений. Тогда можно записать:

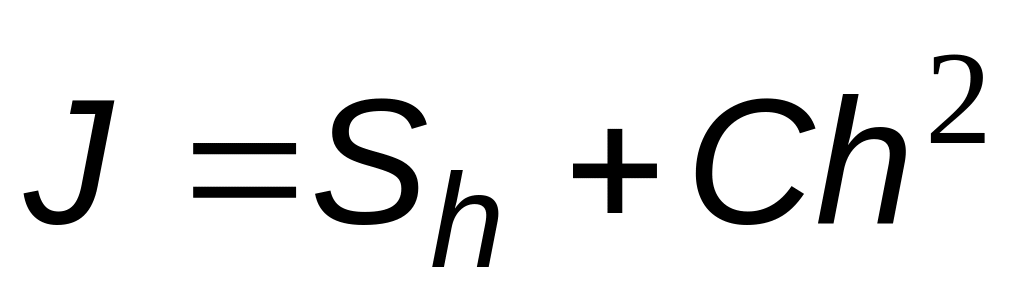и .

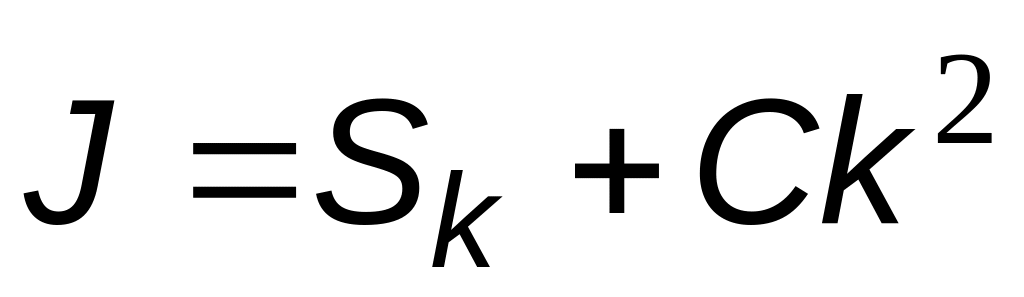(6.19)

Если вычесть эти два уравнения друг из друга, то можно определить С:

.

Тогда, подставляя это значение С в одну из формул (6.19), получаем:

Вычисленное таким образом значение интеграла является гораздо лучшим приближением, чем  S_h или S_k.

Этот метод называется экстраполяционным переходом к пределу или уточнением по Ричардсону.

6.5. М е т о д С и м п с о н а

В этом методе подынтегральная функция заменяется интерполяционным полиномом второй степени  - т.е. параболой, проходящей через точки , , , где i = 0,1,2,...,n-2; , т.е.

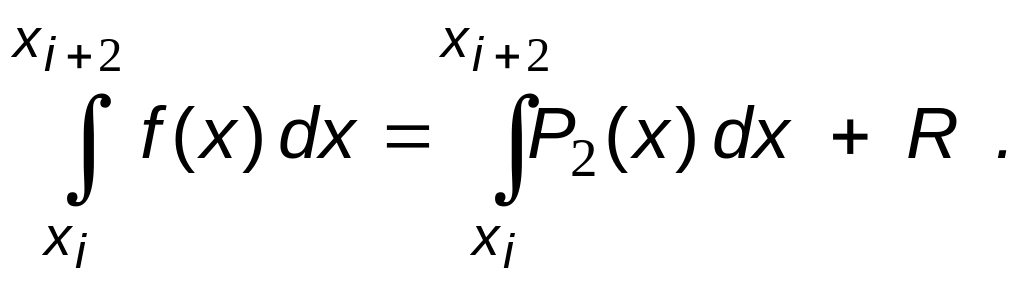
(6.20)

Поэтому данный метод еще называют методом парабол.

Для записи полинома воспользуемся интерполяционной формулой Ньютона (см. раздел 5.Аппроксимация зависимостей) для трех узлов (на примере i=0, i+1=1, i+2=2):

(6.21)

где f₀₁, f₀₁₂ - разделенные разности:

;

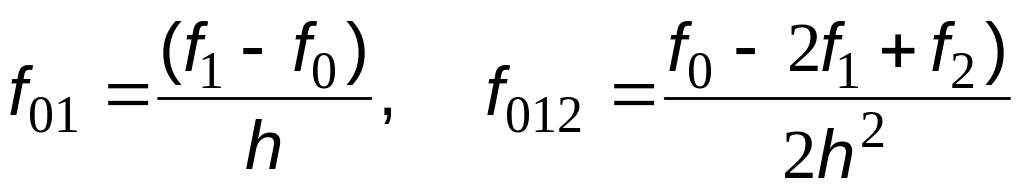(6.22)

h - шаг разбиения промежутка интегрирования.

Введем новую переменную z =  x - x₀. Тогда x = z + x₀ и полином (6.21) принимает вид:

.

(6.23)

Интеграл от полинома (6.23) с учетом (6.22) имеет вид:

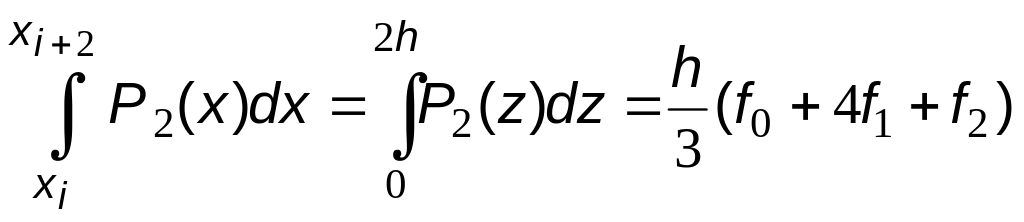
(6.24)

Соотношение (6.24) называют квадратурной формулой Симпсона.

Для всего промежутка интегрирования [ a,b ] при четном значении n количества интервалов его разбиения эта формула имеет вид:

(6.25)

Для удобства программирования эту формулу можно записать так:

,

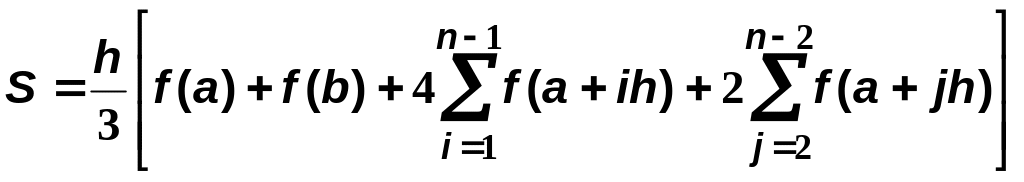причем суммирование идет по нечетным значениям i и по четным значениям j.