4.4. Обращение матриц

Матрица X является обратной по отношению к заданной квадратной матрице A, если их произведение дает единичную матрицу E :

A . X = E .

(4.18)

В единичной матрице элементы главной диагонали равны 1, а все остальные элементы равны 0.

Как известно, произведение двух квадратных матриц A и X порядка n дает квад­рат­ную матрицу C того же порядка, элементы которой вычисляются по формуле:

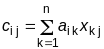
(4.19)

Алгоритм обращения матриц, т.е. вычисления элементов матрицы X, удовлетворяю­щих матричному уравнению (4.18), рассмотрим на примере матриц третьего порядка:

;

;

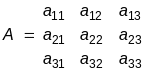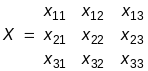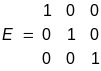
Уравнение (4.18) с учетом формулы (4.19) для этих матриц имеет вид:

a11 x11+a12 x21+a13 x31	a11 x12+a12 x22+a13 x32	a11 x13+a12 x23+a13 x33		1 0 0
a21 x11+a22 x21+a23 x31	a21 x12+a22 x22+a23 x32	a21 x13+a22 x23+a23 x33	=	0 1 0
a31 x11+a32 x21+a33 x31	a31 x12+a32 x22+a33 x32	a31 x13+a32 x23+a33 x33		0 0 1

Фактически здесь записаны три СЛАУ третьего порядка:

	a11 x11 + a12 x21 + a13 x31	=	1
1)	a21 x11 + a22 x21 + a23 x31	=	0
	a31 x11 + a32 x21 + a33 x31	=	0

	a11 x12 + a12 x22 + a13 x32	=	0
2)	a21 x12 + a22 x22 + a23 x32	=	1
	a31 x12 + a32 x22 + a33 x32	=	0

	a11 x13 + a12 x23 + a13 x33	=	0
3)	a21 x13 + a22 x23 + a23 x33	=	0
	a31 x13 + a32 x23 + a33 x33	=	1

Их особенностью является то, что все три системы имеют одну и ту же матрицу коэффициентов при неизвестных, а именно матрицу А.

Итак, чтобы найти матрицу X, обратную к заданной матрице А порядка n, надо решить n систем линейных уравнений, матрицей коэффициентов которых является исходная матрица А, а вектор-столбцами свободных членов являются столбцы еди­ничной матрицы E.

При использовании метода Гаусса решения этих n систем прямой ход можно осу­ществить одновременно для всех систем. Расширенная матрица при этом будет иметь по­рядок n х 2n; ее левая половина есть матрица А, правая - матрица E.