Построение эпюры изгибающих моментов (м)
1 участок: 0 z1 с М1 = P2·z1
при z1 = 0 M1 = 0
при z1 = с = 0,5 м M1 = P2·с = 30·0,5 = 15 кН∙м
2 участок: с z2 с+b M2 = P2·z2 -q2∙(z2-с)∙[(z2-с)/2]= P2·z2-q2∙[(z2-с)2/2]
при z2 = с = 0,5 м M2 = P2·с = 30·0,5 =15 кН∙м
при z2 =с+b=2,5м М2 =P2·(b+с)-q2∙b2/2=30·2,5-24·22/2=75-48=27 кН∙м
Максимальное значение изгибающего момента на 2-ом участке будет при подстановке z2 = z'2 в уравнение M2 = P2·z2-q2∙(z2-с)[(z2-с)/2] = P2·z2-q2∙[(z2-с)2/2]
M2= 30·1,75-24·(1,75-0,5)2/2 = 52,5-18,75 = 33,75 кН∙м
3 участок: с+b z3 с+b+а M3= P2·z3-q2∙(z3-с)[(z3-с)/2]+М= P2·z3-q2∙[(z3-с)2/2]+М
при z3=с+b=2,5м M3=P2·(b+с)-q2∙b2/2+М=30·2,5-24·22/2+20=27+20=47 кН∙м
при z3=с+ b+а=3,5м М3=P2·(в+с+а)-q2(в+а)2/2+М=30·3,5-24·32/2+20=17 кН∙м
По полученным на границах участков и в экстремальной точке значениям М строится эпюра изгибающих моментов.
Максимальный внутренний изгибающий момент Мmax = 47 кН∙м возникает в сечении, где приложен внешний изгибающий момент.
З адача 6. Часть 4
Схема 5
q
2
Р2
М
Дано:
а
= 1 м
b = 2 м Р1
с
= 0,5 м
Р2 = 30кН с Z1 в с 0,5а
М
= 20 кНм
q
2
= 24 кН/м Z2 Z3
Z4
d
42 42
30
12
1 ) Построить эп.Q и М эп.QкН
2
)
Подобрать размеры
сечения по σ -18
3
)
Проверить прочность 34
по τ
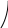
3 15
13
эп.М кНм
-5
Р е ш е н и е:
Построение эпюры q
I участок: 0 z1 с Q1= q2z1
при z1=0 Q1=0 кН
при z1=с=0,5 м Q1=24·0,5=12 кН
II участок: с z2 с+в Q2=q2z2 -Р2
при z2=с=0,5 м Q2=24·0,5-30=18 кН
при z2=с+в=2,5 м Q2=24·2,5-30=30 кН
III участок: в+с z3 2с+в Q3= q2z3 - Р2
при z3=с+в=2,5 м Q3=24·2,5-30=30 кН
при z3=2с+в=3 м Q3=24·3-30=42 кН
IV участок: в+2с z4 2с+в+0,5а Q4= q2(2с+в) - Р2
при z3=2с+в=3 м Q4=24·3-30=42 кН при z4
По полученным значениям Q на границах участков строим эпюру поперечных сил
Найдем Z2 при Q2=0 0=q2z2 -Р2 => z2 = Р2/ q2 =30/24=1,25 м
Построение эпюры м
I участок: 0
z1
с М1=
при z1=0 М1=0
при z1=с=0,5 м М1=24·0,125=3 кНм
II участок: с
z2
с+в
М2=
при z2=с=0,5 м М2=24·0,125-30·0=3 кНм
при z2=с+в=2,5 м М2=24·2,52/2-30·2=15 кНм
при z2= 1,25 м М2=24·1,252/2-30·0,75=-3,75 кНм
III участок: с+в
z3
2с+в М3=
при z3=с+в=2,5 м М3=24·2,52/2-30·2-20 = -5 кНм
при z3=2с+в=3 м М3=24·32/2-30·2,5-20 =13 кНм
IV участок: в+2с
z4
2с+в+0,5а
М4= q2(2с+в)
-М- Р2(z4-c)
при z4=2с+в=3 м М4=24·3(3-1.5)-30·2,5-20=13 кНм
при z4=2с+в+0,5а=3,5 м М4=24·3(3,5-1.5)-30·3-20=34 кНм
По полученным значениям М на границах участков строим эпюру изгибающих моментов