Определение касательных напряжений при поперечном изгибе
При поперечном изгибе наряду с изгибающим моментом в сечении балки возникает поперечная сила (Q). Наличие поперечной силы связано с возникновением в поперечном сечении касательных напряжений.
Касательные напряжения при изгибе не распределяются равномерно на высоте сечения. Формула для подсчета касательных напряжений при изгибе носит название формулы Журавского.
τ
=
где Qy (Q) – поперечная сила в рассматриваемом сечении.
S`x – статистический момент относительно нейтральной оси той части сечения, которая лежит выше или ниже прямой проведенной через данную точку;
Ix – осевой момент инерции всего сечения относительно нейтральной оси.
b – ширина поперечного сечения на уровне точки, в которой определяется напряжение.
Q, Ix, b для сечения постоянной ширины не меняются.
Sx изменяется в зависимости от y1, следовательно, τ в любой точке поперечного сечения зависит только от y1. Касательные напряжения достигают максимального значения:
Для
прямоугольного сечения: τmax
=
в
точках на нейтральной линии (при y
= 0)
Для
двутавра: τmax
=
, где SxП/С
– статистический момент полусечения.
Для
круглого сечения: τmax
=
, где A
– площадь.
Максимальное касательное напряжение для большинства симметричных сечений относительно нейтральной оси (X) имеет место в точках лежащих на нейтральной оси.
Условие прочности по касательным напряжениям: τmax ≤ [τ]
Задача 6. Часть 1
Схема 5
Д
ано:
RA q1 RB
а
= 1 м М
b
= 2 м
с
= 0,5 м В М
Р
1
= 20 кН А
М
= 20 кН·м
q
1
= 10 кН/м
z1
z2
z3
1) Опр-ть
опорные а b с
реакции
2)Построить
эп. Q и М
17,1
7,1
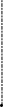эп. Q, 0
0
(кН)
-12,9
z'2 -12,9
12,1
эп.М, 0
0
(кН·м) -5,38
-7,9
-13,7
-20
Решение:
Обозначим опоры, поставим реакции опор.