Совместный спектр двух коммутирующих операторов.
Пусть есть два эрмитовских оператора
и
и они функционально не связаны:
Теорема
1: Если операторы
и
коммутируют
,
то они могут иметь общую систему
векторов.
Теорема 2: Если операторы и имеют общую систему собственных векторов, то они коммутируют.
Доказательство:
Запишем операторы в собственном базисе.
т.к. операторы эрмитовские, то
- и коммутируют.
Рассмотрим два оператора функционально несвязанных.
Пары
чисел
называются совместным спектром двух
операторов.
Допустим, что
значит совместный спектр операторов имеет вырожденные собственные значения.
Может быть:
тогда совместный спектр невырожденный.
Если бы:
,то
Если
,
то
,
но если все таки
,
то совместный спектр оказывается
вырожденным и такое вырождение называется
случайным.
Попробуем
найти третий оператор
такой, чтобы
Совместный спектр оператора состоит из трех чисел.
Совместный
спектр трех операторов уже невырожденный.
Если
,
то нужно искать 4 оператор
коммутирующий с первыми тремя.
Если есть случайные вырождения в совместном спектре операторов, то нужно добавлять операторы коммутирующие с предыдущими и расширять спектр до тех пор пока:
1) не снимется вырождение совместного оператора
2) не закончатся операторы.
Набор операторов совместный спектр которых оказывается простым, называется полным набором операторов.
Собственные векторы, полученные для операторов входящих в простой спектр образуют полную систему линейно независимых векторов.
Функциональные векторные пространства.
в качестве векторов
выступают функции.
Если есть граница области, то должны быть заданы граничные условия, которые должны удовлетворять функции.
- кратчайшее
расстояние между двумя точками.
gij - метрический тензор
Операторы функциональных пространств.
1) оператор координаты
2) оператор дифференцирования
- оператор импульса
3) оператор инверсии
4) оператор Лапласа
5) оператор трансляции
В
многомерном пространстве:
6) единичный оператор
Представление операторов интегральным ядром.
D – область значений x’.
х и х’ – n мерные векторы
T(x, x’) – интегрально ядро.
Интегральное ядро единичного оператора. Дельта – функция Дирака.
- интегральное ядро единичного оператора (дельта – функция)
Свойства:
1)
2) f(x)=1 – взяли некоторую функцию f(x)
Мы проинтегрировали по x’, но x в ответ не входит, это может быть тогда, когда:
3) Интегрируем по всей оси x’, а получаем значение f(x) в точке x.
Если здесь будет конечное число, то умножение его на бесконечно малый интервал даст нам 0.
4)
определяем как симметричную.
Пик бесконечно узкий и бесконечно высокий. Толщина и высота определяются выражением:
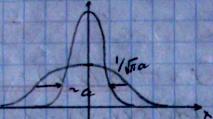
Аппроксимация дельта – функции другими функциями.
1)
Высота
=
,
чтобы площадь под этой функцией = 1.
когда n=2k+1, I=0
когда n=2k, I удваивается
2)
a – ширина Гаусовского колокола
- условие нормировки.
Если дельта – функция зависит от функции
Если нулей у F(x) нет, то дельта – функция от F равна 0.