Теория линейных операторов в гильбертовом пространстве. Векторное пространство.
Общие свойства:
V – векторное пространство
Вектор – элемент векторного пространства.
-
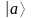ket
вектор
1) в векторном пространстве должна быть определена операция суммы
Правило, по которому 2 векторам из V ставится в соответствие вектор из V.
2) в векторном пространстве должна быть определена операция умножения вектора на число
3) в векторном пространстве должен быть определен обратный вектор
4)
Примеры векторных пространств:
1)
2)
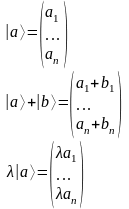
3)
Линейная независимость векторов.
в том случае, когда
данное уравнение выполняется только
лишь при всех
,
векторы
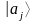называются линейно независимыми. Если
равенство выполняется хотя бы при одном
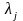отличным от нуля, то система векторов
является линейно зависимой.
Размерность векторного пространства.
Берем
m векторов из векторного пространства
и проверяем их на л/независимость.
- линейно независимы. Добавляем еще
один вектор к системе и проверяем будет
ли система линейно независимой.
Продолжаем до тех пор, пока мы не сможем
найти вектор, который делает систему
линейно независимой.
mmax – максимальное количество линейно независимых векторов называется размерностью пространства.
Любой набор, состоящий из max количества линейно независимых векторов, называется базисом пространства.
базис:
j=1,
2, 3,… n
сепарабельное векторное пространство (если число элементов базиса счетно).
При этом n может быть = ∞, тогда пространство сепарабельное, но бесконечномерное.
k меняется непрерывно, тогда вектора a(k) пересчитать нельзя и пространство несепарабельно.
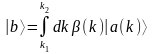- несепарабельное
пространство
β – коэффициент разложения
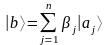в
случае сепарабельного пространства.
Также
бывает
-
смешанное пространство
Сопряженное векторное пространство.
Скалярное произведение векторов.
V* - сопряженное пространство
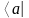- bra
вектор
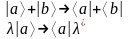
Скалярным произведением двух векторов называется число со следующими свойствами:
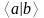- ортогональные,
если скалярное произведение обращается
в ноль.
Если норма вектора = 1, то такой вектор нормированный или единичный.
Пример:
Ортонормированный базис.
Выберем в качестве базиса набор векторов:
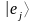- единичный вектор
- при данном условии
базис будет ортонормированным.
Разложим a и b по базису. Тогда:
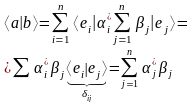
Построение ортонормированного базиса.
Имеем систему линейно независимых векторов.
- хотим сделать его ортонормированным.
Линейные операторы.
Оператор
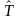называется линейным, если выполняется
следующее равенство:
- оператор импульса
- оператор трансляции
- оператор инверсии
-
оператор Павлова
Матричные элементы оператора.
Можем составить скалярное произведение
-
матричный элемент оператора.
- матричный элемент
посчитанный на базисных векторах.
Как действует оператор на базис:
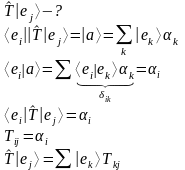
Как связаны компоненты векторов:
Как посчитать матричный элемент в функциональном векторном пространстве:
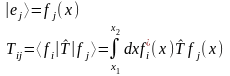
Представление оператора через свои матричные элементы.
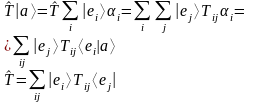
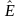- единичный оператор
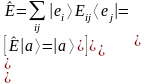
Получили матрицу, которая в пространстве векторов образует оператор.
Функциональные векторные пространства.
Интегральное ядро оператора.
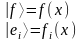
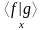- имеем дело со
скалярным произведением и аргументы
одинаковые.
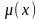- весовая функция
,
пространство бесконечномерное, то это
пространство гильбертово.
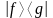- просто алгебраическое
произведение функций.
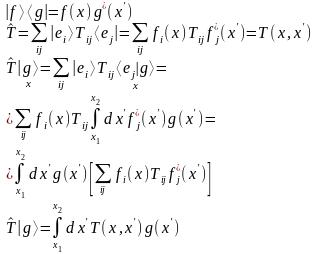T(x,x’)
– интегральное ядро оператора Т.
Действия над операторами.
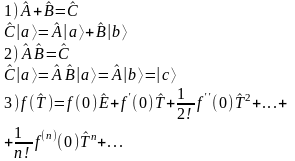
Функция от оператора – оператор.
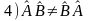
Можно построить коммутатор:
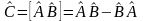
Если коммутатор = 0, то операторы А и В коммутирующие.
порядок действия операторами на вектор имеет значение.
Свойства коммутаторов.
-
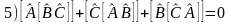тождество Якоби.
Сопряженные операторы.
Если есть векторное пространство V, то существует сопряженное векторное пространство.
сопряженный оператор переводит соответствующие векторы друг в друга в сопряженном векторном пространстве.
Берем комплексное сопряжение и транспонирование.
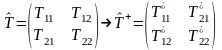
Если Т+=Т, то Т – эрмитовский или самосопряженный.
Оператор Паули:
Преобразование базиса. Унитарные операторы.
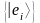- ортонормированный
базис.
Хотим
перейти к другому базису
.
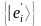Оператор, переводящий векторы одного базиса в векторы другого – унитарный оператор.
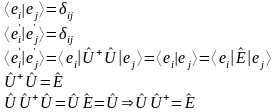
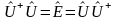- определение
унитарного оператора.
Введем вектор:
Скалярное произведение не меняется в результате унитарного преобразования.
Унитарный оператор не меняет длины вектора.
Преобразование компонент вектора при унитарном преобразовании.
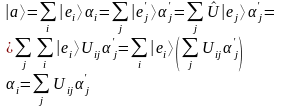
Преобразование матричных элементов при унитарном преобразовании.
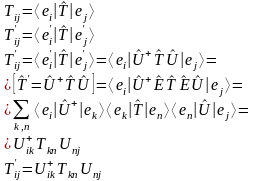
Обратный оператор.
Если
есть оператор
,
то существует обратный оператор
,
который удовлетворяет условию:
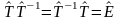
- для унитарного оператора.
Проекционный оператор.
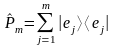
Есть векторы ортонормированного базиса
- полная система
линейно независимых векторов.
- единичный оператор
m<n
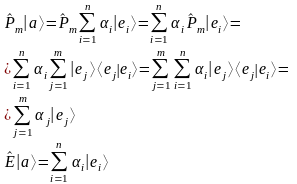
Суммы отличаются количеством слагаемых.
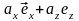- проекция
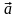на плоскость XOZ.
проектирует вектор
на какое-то m
мерное подпространство пространства
n.
Возьмем базис векторов на плоскости:
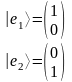
Составим проекционный оператор:
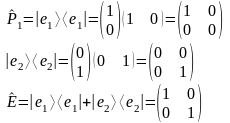
Подействуем оператором на вектор в матричной форме:
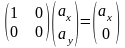
- определение единичного оператора и условие полноты базиса.
Если получаем единичный оператор, значит набор базисных векторов полный.
Возведем в квадрат:
