22. Сформулируйте неравенство Чебышева. Что такое «общее правило трёх сигм»?

Н-во Чебышева: Пусть X – СВ, у кот есть M(X)=m и D(X)=a, тогда  >0 справедливо неравенство:

P(|X-m|)  D(X)/²

Правило 3: Для любой СВ Х выполняется неравенство P(|X-m|<3) 8/9.

Пусть =3. Тогда P(|X-m|<3)  1-²/9² = 8/9.

23. Сформулируйте центральную предельную теорему. Укажите примеры ее применения.

ЦПТ для одинаково распределенных СВ: Пусть X₁…X_n – последовательность независимых одинаково распределенных СВ M(X₁)=…=M(X_n)=m<+; D(X₁)=…=D(X_n)=²<+, тогда закон распр СВ

S_n = (x₁+…+x_n – nm)/√n, тогда S_n стремится к стандартному нормальному закону при n→ {

Применение: При измерении какой-либо физ величины на результат влияет огромное кол-во факторов. Каждый из этих факторов порождает ничтожную ошибку Xk. Результирующая ошибка Sn будет суммой величин Xk, то есть вся сумма Sn будет иметь закон распределения, близкий к нормальному. Сл-но, случайная ошибка измерения подчиняется нормальному закону распр: мат ожидание равно нулю, среднее квадратич откл – характеризует точность измерения. Др. пример: массовое производство. Изготовляются большие партии однотипных изделий, где каждое должно соответствовать стандарту. Но есть отклонение от стандарта, кот порождаются причинными случайного хар-ра (Xk). Sn имеет норм распр.

24. Пусть X – дискретная случайная величина, принимающая только неотрицательные значения и имеющая математическое ожидание m . Докажите, что P(X ≥ 4) ≤ m/4 .

m= (т.к. 1-ое слагаемое положительно, то если его убрать, будет меньше)  (заменим a на 4, будет только меньше)  = =4P(X4). Отсюда P(X ≥ 4) ≤ m/4 .

(Вместо 4 может быть любое число).

25. Сформулируйте понятие состоятельной оценки параметра генерального распределения. Приведите пример.

Оценка называется состоятельной, если она стремится (по вероятности) к оцениваемому параметру.

Выборочное среднее

является состоятельной оценкой для генерального среднего.

26. Как вводятся основные характеристики статистической совокупности (выборки): среднее, дисперсия, центральные моменты высших порядков, асимметрия, эксцесс? Какие из перечисленных характеристик остаются неизменными при линейных преобразованиях x → ax + b?

Центральным моментом порядка k (k е N) случайной величины X называют мат. ожидание k-й степени отклонения = X – m, где m – мат. ожидание X:

1. 

Для дискретных случайных величин формула для центрального момента порядка k выглядит следующим образом:

для непрерывных случайных величин

Асимметрией распределения называют отношение третьего центрального момента к кубу стандартного отклонения:

Замечание. Асимметрия случайной величины X совпадает с третьим начальным (центральным) моментом соответствующей нормированной случайной величины.

Действительно, по определению

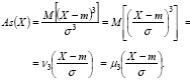
Эксцессом распределения называется величина

Поскольку для стандартного нормального распределения N(0, 1) мы нашли, что μ₄ = 3, то для нормального распределения эксцесс равен нулю. В частности, вычисляя эксцесс неизвестного распределения, мы можем судить о близости его к нормальному по этой числовой характеристике.

Для биномиального закона

Действительно, воспользуемся формулой. Имеем

Дисперсией случайной величины X называется число

Другими словами, дисперсия есть математическое ожидание квадрата отклонения.

Из определения легко вытекают следующие свойства дисперсии.

остаются неизменными при линейных преобразованиях x → ax + b Дисперсия, асимметрия, эксцесс.