12. Перечислите основные свойства функции плотности вероятности. Чем объясняется название «плотность вероятности»?

Св-ва плотности:

1. f(x)

2. 

3. во всех точках, где ф-ция плотности непрерывна вып. равенство

f(x)=F’(x)

Поясним смысл назв. «плотность вероят-ти»

по т. о среднем интеграле, стоящ. в прав. части, равен , где некоторая точка из инт. .

Отсюда

Представим себе, что инт. , стягив. к некоторой точке , причем в этой точке функция f(x) непрерывна. Тогда будет стремиться к числу f( ), и мы получим:

Отношение, стоящее под знаком предела, есть своего рода «вер-ть на ед-цу длины» интервала . Предел этого отношения рассмотрим как плотность вероятности в самой т. . Во всякой т. , где f(x) непрер., число f(x) совп. с поним-й плотностью вер-ти в т. . Что и требовалось доказать.

13. Запишите плотность распределения нормальной случайной величины x, для которой М(x)=m, D(x)=δ². Как изменится график плотности распределения, если: а) увеличится m, б) увеличится δ?

а) известно, что графики функций f(x) и f(x-a) имеют одинаковую форму: сдвинув график f(x) в положительном направлении оси x на а единиц масштаба при а<0 получим график f(x-a). Отсюда следует, что изменение величины параметра m (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к её сдвигу вдоль оси Ох. При увеличении m график плотности сдвинется вправо.

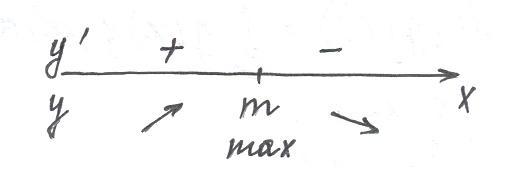
2) Исследуем функцию на экстремум.

f’(x)=0 при x=m

При x=m функция имеет максимум

С возрастанием δ максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси Ох.

14. Как вычисляется математическое ожидание в случае распределения с плотностью f(x)? Может ли для какой-либо абсолютно непрерывной случайной величины не существовать математического ожидания? Ответ обоснуйте.

Математическое ожидание абсолютно непрерывной СВ Х с функцией плотности f(x) определяется равенством: М(Х)= интеграл xf(x)dx от минус беск до плюс беск

Мат. ожиданием случайной величины Е называется число . Если указанный справа предел не существует, то мат. ожидание величины х также считается несуществующим.

Если дискретная случайная величина Х принимает счетное множество возможных значений, то , причем мат. ожидание существует, если ряд в правой части равенства сходится абсолютно. Т.к. ряд может и расходиться, то соотв. случайная величина может и не иметь мат. ожидания. На практике, как правило, множество возможных значений случайной величины распространяется лишь на ограниченный участок оси абсцисс и, значит, мат. ожидание существует.

15. Как вычисляется дисперсия в случае распределения с плотностью f (x)? Что можно сказать о случайной величине Х в случае D(X) = 0?

16. Перечислите основные свойства математического ожидания. Докажите, что если график плотности вероятность f(x) случайной величины X симметричен относительно прямой х = а и М(Х) существует, то М(х) = а.

Математическое ожидание имеет следующие свойства:

1. Математическое ожидание случайной величины равно ей самой: М(С)=С

2. Постоянный множитель можно вынести за знак математического ожидания: М(сХ)=сМ(Х).

Следовательно: M(aX+bY)=aM(X)+bM(Y)

3. Математическое ожидание суммы случайных величин равно сумме их мат. Ожиданий:

4. Если случайные величины независимы, то мат. ожидание их произведений равно произведению их мат. ожиданий:

5. Мат. ожидание от функции равно:

Математическое ожидание случайной величины Х:

M(X) = ∫_{(верх. +∞, нижн. -∞)} x ф_N (x) dx = ∫_{(верх. +∞, нижн. -∞)} x (1/σ * _{кв.корень из} 2π) * {е _{в степени} -((x – a)^2)/2*σ^2)} * dx. Произведем замену переменной, положив t = (x – a)/(σ * _{кв.корень из} 2). Тогда x = a + (σ * _{кв.корень из} 2) * t и dx = (σ * _{кв.корень из} 2) * dt, переделы интегрирования не меняются, и следовательно,

M(X) = ∫_{(верх. +∞, нижн. -∞)}(1/σ * _{кв.корень из} 2π)*(a + (σ * _{кв.корень из} 2) * t) * (е _{в степени} –t^2) * (σ * _{кв.корень из} 2) * dt = (σ * _{кв.корень из} 2) / _{кв.корень из} π) ∫_{(верх. +∞, нижн. -∞)} t*(е _{в степени} –t^2) * dt + (a/ _{кв.корень из} π) ∫_{(верх. +∞, нижн. -∞)}(е _{в степени} –t^2) * dt = 0 + (a/_{кв.корень из} π) * _{кв.корень из} π = a. Первый интеграл = 0 как интеграл от нечетной функции по симметричному относительно начала координат промежутку, а второй интеграл ∫_{(верх. +∞, нижн. -∞)}(е _{в степени} –t^2) * dt = _{кв.корень из} π – интеграл Эйлера – Пуассона.