1. Что такое случайное событие, связанное с опытом? Приведите примеры. Имеет ли смысл сумма(произведение событий относящихся к разным опытам?)

Случайным событием называется любой факт, который в результате испытания может произойти или не произойти. Под испытанием (опытом) понимается выполнение определенного комплекса условий, в которых наблюдается то или иное явления, фиксируя тот или иной результат.

Примеры: Выигрыш автомобиля по билету лотереи. Выход бракованного изделия с конвейера предприятия.

Нет, не имеет, т.к. сумма/произведение связаны с разными опытами. У них различны область и элементарные исходы.

2. Что такое правило умножения вероятностей?

Правило: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло.

Р(ABC…KL)=P(A) * Pa(B) * Pab(C) … Pabc..k(L)

3. Является ли равенство P(ABC) = P(A) * P(B) * P(C) достаточным для независимости событий A,B и С? Ответ обосновать.

Нет, не является. Т.к. попарная независимость нескольких событий (т.е. независимость взятых из них двух любых событий) еще не означает их независимости в совокупности. Это нам покажет следующий пример:

Грани правильного тетраэдра окрашены. 1-я (А) в красный цвет, 2-я (В) в зелёный, 3-я (С) в синий и 4-я во все 3 цвета (событие АВС). При его подбрасывании вероятность любой грани, на которую он упадет, в своей окраске иметь одинаковый цвет = ½. Таким образом, Р(А) = ½, P(B) = ½, Р(С) = ½. Точно также можно посчитать, что Pb(A) = Pc(A) = Pa(B) = Pc(B) = Pa(C) = Pb(C) = ½ (один шанс из двух), т.е. события А,В и С попарно независимы. Если же наступили одновременно два события, например А и В, т.е. АВ, то событие С обязательно наступит, т.е. Раb(С) = 1 и аналогично Рас(В) = 1, Рbc(А) = 1. Следовательно, вероятность каждого из событий А,В или С изменилась, и события А,В и С в совокупности зависимы.

4. Что такое полная группа событий? Приведите пример, когда события ав, āв и не образуют полной группы событий.

Полная группа событий - это система случайных событий такая, что в результате произведённого случайного эксперимента непременно произойдёт одно из них. АВ, А*В, А*+В* (чёрточка одна на А и В)-не образуют полной группы событий. А*+В*(чёрточка одна на А и В)=А*В*. Полную группу событий составляют: АВ, А*В, АВ*, А*В*. Сл-но АВ, А*В, А*В* - не образуют полной группы.

Пример: студент сдаёт 2 зачёта, соб.А- сдан 1 зачёт, соб.В- сдан 2 зачёт, Р(А)=1/2, Р(В)=2/3

Р(АВ+А*В+А*В*)≠1, т.к. Р(АВ*)≠0, сл-но соб. АВ, А*В, А*+В* (чёрточка одна на А и В)-не образуют полной группы.

5. Пусть 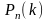- вероятность k успехов в серии n независимых испытаний с вероятностью успеха p в каждом испытании. При каком k вероятность достигает максимума? Совпадает ли это число с математическим ожиданием количества успехов?

Рассмотрим два соседних числа и . Между ними имеет место одно из соотношений: (меньше, равно или больше) или, что эквивалентно, . Подставляя вместо числителя и знаменателя их выражения по формулам , или учитывая, что , получим соотношения или . Собирая все слагаемые с множителем k и учитывая , что p+q=1 , получим эквивалентные соотношения . Обозначим число np+p через . Тогда перепишется : .

Таким образом, для всех значений k меньших чем справедливо неравенство , для ( это возможно только в том случае, когда - целое число) имеет место равенство , наконец, при выполняется неравенство . Тем самым при значениях функция возрастает, а при значениях убывает. Следовательно, если число не является целым, то функция имеет единственный максимум; он достигается при ближайшем к слева целом значении k , т.е. при таком целом 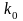, которое заключено между -1 и :

np-q< <np+p, =[np+p].

Если же - целое число, то два равных между собой максимума достигается при и .

Если число не является целым, то наиболее вероятное число успехов равно ближайшему к слева целому числу. В случае когда есть целое число, наиболее вероятное число успехов имеет два значения: -1 и .