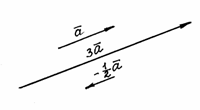- •2. Квадратные матрицы. Транспонирование матриц. Определитель квадратной матрицы. Свойства определителя.
- •3.Минор и алгебраическое дополнение.
- •4.Правила вычисления определителя матрицы произвольной размерности.
- •5.Перемножение матриц.
- •6.Ранг матрицы. Элементарные преобразования над матрицами.
- •7.Системы линейных алгебраических уравнений.
- •10. Метод Крамера решения системы линейных алгебраических уравнений.
- •11.Обратная матрица. Определение и способы вычисления.
- •Метод обратной матрицы решения системы линейных алгебраических уравнений.
- •13.Отыскание решений системы линейных алгебраических уравнений в общем случае.
- •14. Векторы. Определение и линейные операции над векторами.
- •15.Линейная зависимость и независимость векторов.
- •27. Система координат на плоскости. Преобразования системы координат.
- •28. Линии на плоскости. Различные уравнения линий на плоскости.
- •29.Уравнения прямой на плоскости. Различные уравнения прямой на плоскости.
- •30. Угол между двумя прямыми на плоскости. Расстояние от точки до прямой.
- •Линии второго порядка на плоскости. Эллипс.
- •32.Линии второго порядка на плоскости. Гипербола.
- •33 Линии второго порядка на плоскости. Парабола.
- •Поверхность в пространстве. Ее явное и неявное уравнения.
- •Различные уравнения плоскости в пространстве. Угол между двумя плоскостями.
- •36.Различные уравнения прямой линии в пространстве.
- •37. Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых. Условия, при котором две прямые лежат в одной плоскости.
- •38. Угол между прямой и плоскостью. Условие параллельности и перпендикулярности прямой и плоскости.
- •40. Поверхности второго порядка.
13.Отыскание решений системы линейных алгебраических уравнений в общем случае.
1)Рассмотрим
на примере применение теоремы Кронекера
– Капелли для определения совместности
системы линейных уравнений.
Пример.
Выясните,
имеет ли система линейных
уравнений 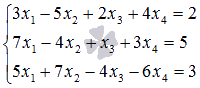 решения.
Решение.
Найдем
ранг основной матрицы системы
решения.
Решение.
Найдем
ранг основной матрицы системы  .
Воспользуемся методом окаймляющих
миноров. Минор второго порядка
.
Воспользуемся методом окаймляющих
миноров. Минор второго порядка 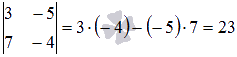 отличен
от нуля. Переберем окаймляющие его
миноры третьего порядка:
отличен
от нуля. Переберем окаймляющие его
миноры третьего порядка:
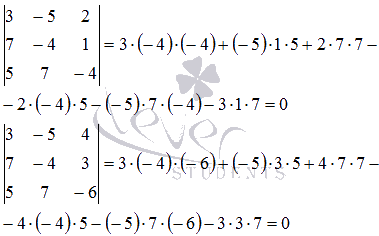 Так
как все окаймляющие миноры третьего
порядка равны нулю, то ранг основной
матрицы равен двум.
В свою очередь
ранг расширенной матрицы
Так
как все окаймляющие миноры третьего
порядка равны нулю, то ранг основной
матрицы равен двум.
В свою очередь
ранг расширенной матрицы 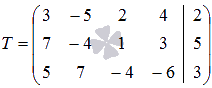 равен
трем, так как минор третьего
порядка
равен
трем, так как минор третьего
порядка
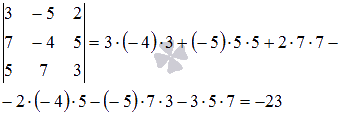 отличен
от нуля.
Таким образом, Rang(A)
< Rang(T),
следовательно, по теореме Кронекера –
Капелли можно сделать вывод, что исходная
система линейных уравнений
несовместна.
Ответ:
система решений не имеет.
отличен
от нуля.
Таким образом, Rang(A)
< Rang(T),
следовательно, по теореме Кронекера –
Капелли можно сделать вывод, что исходная
система линейных уравнений
несовместна.
Ответ:
система решений не имеет.
14. Векторы. Определение и линейные операции над векторами.
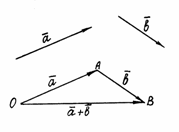
Под вектором в элементарной математике понимают направленный отрезок.
Линейные операции над векторами |
Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число. Сложение
векторов. Пусть
Рис. 1 Ту
же сумму можно получить иным способом.
Отложим от точки О векторы
и
Рис. 2 Понятие суммы можно обобщить на случай любого конечного числа слагаемых (рис. 3).
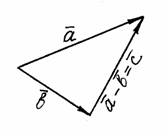
Рис. 3 Вычитание
векторов. Разностью Если векторы и привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого» к «уменьшаемому» (рис. 4).
Рис. 4 Таким
образом, если на векторах
и
,
отложенных из общей точки О, построить
параллелограмм ОАСВ, то вектор
,
совпадающий с одной диагональю, равен
сумме
,
а вектор
Рис. 5 Умножение
вектора на число. Произведением вектора
на
действительное число 1) 2) Очевидно,
что при Построим,
например, векторы
Рис. 6 Из определения следует: два вектора и коллинеарны тогда и только тогда, когда имеет место равенство : |
|
|