4 Практическое занятие №4. Методики проверки гипотезы нормальности распределения.

4.1 Основные понятия и определения

При обработке экспериментальных данных в науке и технике обычно предполагают нормальный закон распределения случайных величин.

Свойства нормально распределенной случайной величины x:

- ;

- плотность вероятности является непрерывной функцией;

- центр распределения случайной величины одновременно является центром симметрии;

- малые отклонения встречаются чаще больших (с большей вероятностью).

Наиболее полной характеристикой случайной величины является закон распределения вероятностей случайной величины, который связывает данное значение случайной величины с вероятностью появления его (т.е. этого значения) в опыте. Наиболее распространенным является закон распределения, получивший название нормального. В аналитическом виде этот закон выражается известным уравнением Гаусса:

, (4.1)

где - плотность вероятностей при данном значении х.

Графически это уравнение имеет вид колоколообразной кривой, которая симметрична относительно центра распределения, которым является Мх (максимум функции ) и концы которой уходят в  , асимптотически приближаясь к горизонтальной оси х и не достигая ее.

При обработке экспериментальных данных если закон распределения генеральной совокупности, из которой взята наша выборка, неизвестен, то первое, что надо сделать - это проверить распределение в выборке на нормальность, т.е. соответствие закону нормального распределения.

Предположение о подчинении выборки на соответствие закону нормального распределения можно сделать:

1. По коэффициенту вариации (2.13).

Если коэффициент вариации превышает 33%, говорить о нормальности распределения данных выборки нельзя.

Предварительный анализ с помощью коэффициента вариации дает самую грубую оценку.

2. По коэффициентам эксцесса и ассиметрии (2.11 - 2.12).

Для нормально распределенной случайной величины коэффициенты эксцесса и асимметрии равны 0. Поэтому, если соответствующие эмпирические величины достаточно малы, можно предположить, что генеральная совокупность распределена по нормальному закону.

3. По несмещенным оценкам для показателей асимметрии и эксцесса.

Для этого необходимо определить несмещенные оценки для показателей асимметрии и эксцесса по формулам 4.2 и 4.3 соответственно:

(4.2)

(4.3)

Определяют среднеквадратические отклонения для показателей асимметрии и эксцесса по формулам 4.4 и 4.5 соответственно:

(4.4)

(4.5)

Проверяют условия:

(4.6)

(4.7)

Если условия выполняются, то гипотеза нормальности распределения принимается

4. Для не очень больших выборок (n<120) можно вычислить среднее абсолютное отклонение (САО):

, (4.8)

где n – объем выборки;

- среднее значение выборки.

Для выборки, имеющей приближенно нормальный закон распределения, должно выполняться условие:

(4.9)

5. Проверку гипотезы нормальности распределения для сравнительно широкого класса выборок (3<n<1000) можно выполнить с помощью метода, основанного на размахе варьирования R.

Подсчитывают отношение , где R – размах варьирования (ширина интервала), - несмещенной оценки дисперсии теоретического распределения (2.6) и сопоставляют с критическими верхними и нижними границами этого отношения (Приложение ).

Если данное отношение меньше нижней границы или больше верхней границы, то нормального распределения нет. Как правило это условие проверяется при 10%-ном уровне значимости.

6. Проверку гипотезы нормальности распределения можно провести по критерию χ².

Для этого необходимо:

- разбить массив исходных данных на классы по формуле 1.1.

- определить середины классов x по формуле 1.4.

- подсчитать частоты для всех классов В (наблюдаемая абсолютная частота);

- вычислить для всех классов Вх и Вх²;

- определить по формулам:

(4.10)

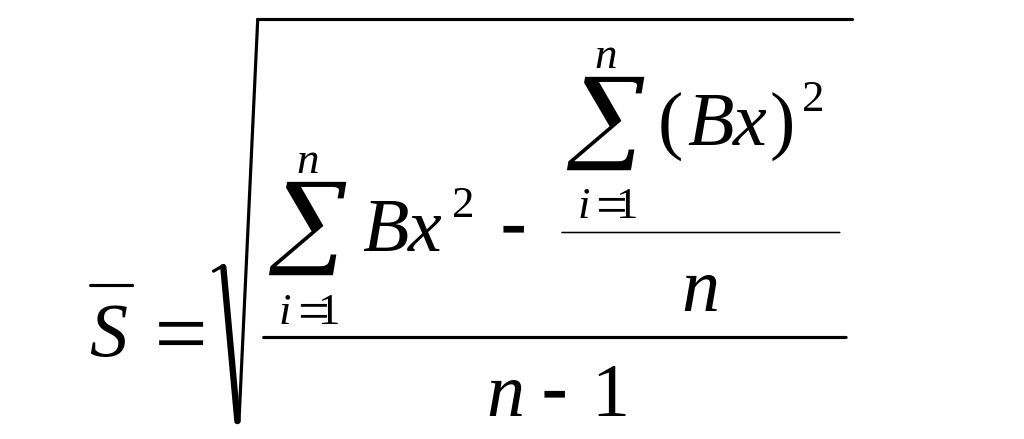(4.11)

- вычислить

(4.12)

- определить

(4.13)

- формируют с помощью таблицы (ординаты стандартной нормальной кривой) вектор столбец f(z);

н) вычисляют для всех классов f(z)k^’, , , где Е= f(z)k' ожидаемая по стандартному нормальному распределению частота.

Если в каком-либо классе число наблюдений окажется меньше четырех, то его объединяют с соседним классом (классами) так, чтобы число наблюдений в таком объединенном классе оказалось большим или равным четырем.

о) вычисляют χ² по формуле (4.14)

п) проверяют, используя таблицу ( процентные точки распределения χ²) условие χ²< χ²_(ν;p), где ν = n_кл -1 -2; p=0,10