2 Практическое занятие №2. Вычисление характеристик эмпирических распределений (выборочных характеристик).

2.1 Основные понятия и определения

Для компактного описания совокупности наблюдений (результатов измерений характеристик) используют методы описательной статистики (описания результатов с помощью различных агрегированных показателей и графиков).

Показатели описательной статистики можно разбить на несколько групп:

1) показатели положения – описывают положение экспериментальных данных на числовой оси. К таким показателям относятся:

- max и min элементы выборки;

- среднее выборочное;

Пусть имеется ряд наблюдений х₁ , х₂, х₃, ….х_n непрерывно распределенной случайной величины, тогда среднее значение наблюдаемого признака (выборочное среднее) определяется по формуле:

, где (2.1)

х_i - значение наблюдаемого признака;

n - объем выборки.

- медиана – значение исследуемого признака, справа и слева от которого находится одинаковое число упорядоченных элементов выборки.

Если объем выборки (n) – четное число, то медианой является среднее арифметическое двух центральных членов:

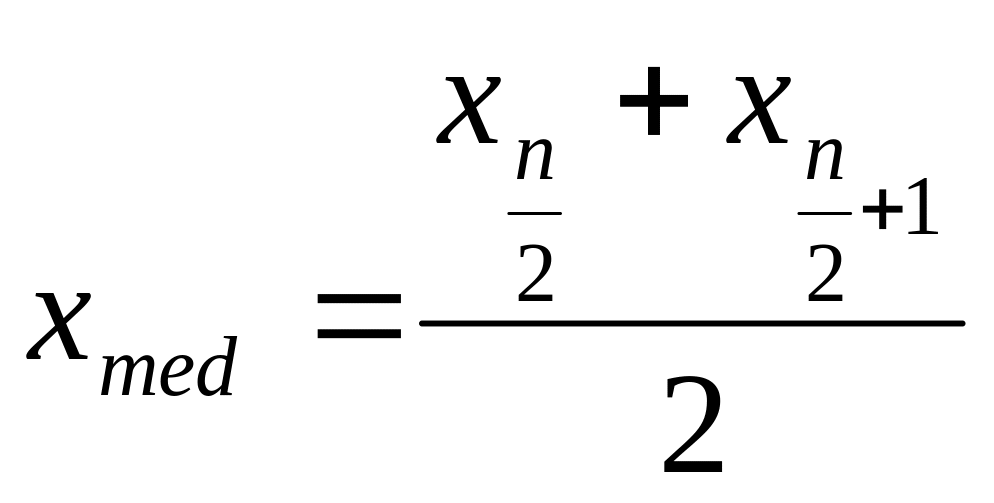(2.2)

Если n - нечетное, то:

(2.3)

- мода – значение признака, которому соответствует наибольшая частота.

2. показатели разброса – описывают степень разброса данных относительно своего центра (среднего значения).

К ним относятся, например:

- размах, варьирование или интервал выборки – разность между max и min элементами выборки;

- выборочная дисперсия или дисперсия эмпирического распределения, рассчитывается как сумма квадратов разности между элементами выборки и средним значением:

, (2.4)

где - отклонение каждого наблюдения от среднего.

Дисперсия характеризует разброс элементов выборки вокруг среднего значения.

- среднеквадратические отклонения:

а) для дисперсии эмпирического распределения:

(2.5)

б) для несмещенной оценки дисперсии теоретического распределения σ² (для генеральной совокупности):

, где (2.6)

Оценка называется несмещенной, если при любом числе наблюдений n ее математическое ожидание точно равно значению оцениваемого параметра.

- центральные моменты распределения – отклонение отдельных величин признака от его средней арифметической величины:

а) первый центральный момент равен:

(2.7)

б) второй центральный момент равен:

(2.8)

в) третий центральный момент равен:

(2.9)

г) четвертый центральный момент равен:

(2.10)

- и другие;

3) показатели асимметрии – положение медианы относительно среднего:

- коэффициент эксцесса, является характеристикой того, насколько кучно основная масса данных группируется около центра и является характеристикой поведения плотности (полигона) в районе её модального значения:

(2.11)

Для нормального распределения .

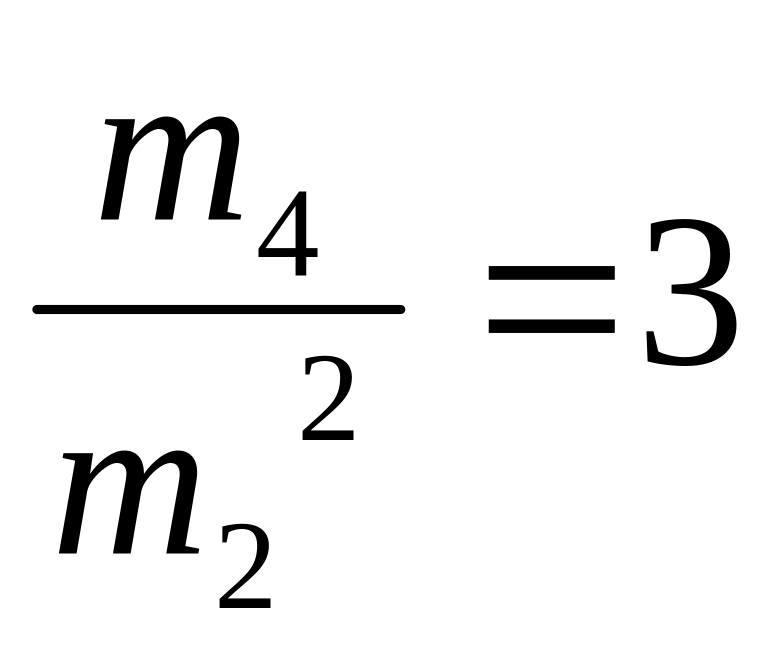Аналогом отсчета в измерении степени островершинности служит нормальное распределение, для которого g₂=0.

Для островершинных (по сравнению с нормальным распределением) g₂>0, а для плосковершинного g₂<0 .

- коэффициент асимметрии, характеризует асимметричность распределения;

Выборочный коэффициент асимметрии является характеристикой степени скошенности и подсчитывается с помощью второго и третьего выборочных центральных моментов:

(2.12)

Для симметричных распределений m₃ = 0 и g = 0.

4) коэффициент вариации - является мерой относительной изменчивости наблюдаемой случайной величины:

(2.13)

Если коэффициент вариации υ<33%, то выборка подчиняется нормальному закону распределения.

5) гистограмма (и любые другие графики).