Центробежные и осевые компрессоры
11. Лопастные компрессоры
Лопастные компрессоры выпускаются промышленностью в двух вариантах: центробежные и осевые, схемы движения газа в которых различны. Поэтому рассмотрение работы каждой машины произведено отдельно.
Принцип работы лопастных машин состоит в том, что поток газа разгоняется в рабочем колесе до высокой скорости, а, затем, в диффузоре скорость потока уменьшается и часть скоростной составляющей полной удельной работы преобразуется в статическое давление.
Преимуществом таких компрессоров перед поршневыми: в них отсутствует поступательное движение рабочего органа, а, значит, нет инерционных усилий и вибрации, которые передаются фундаменту, уменьшаются массо-габаритные показатели установки, нет загрязнения сжатого газа продуктами смазки и т.д.
11.1. Схема движения потока в рабочем колесе центробежной машины
При вращательном движении рабочего колеса поток газа в межлопаточном канале по отношению к неподвижному наблюдателю является абсолютным, а по отношению к лопатке колеса – относительным.
Струйная теория идеального колеса рассматривает движение потока через колесо, имеющего бесконечное число бесконечно тонких лопаток. В этом случае, при пренебрежении изменением потенциальной энергии, уравнение Бернулли можно представить в виде
const,
(111)
где р – давление, Па; с – скорость движения потока, м/с; ρ – плотность среды, кг/м3.
При струйном движении план скоростей в центробежном колесе приведен на рис.33.
Примем обозначения:
u1, u2, - векторы окружных скоростей частиц потока соответственно на входе и выходе рабочего колеса, м/с;
w1, w2 – векторы относительных скоростей при входе и выходе колеса, м/с;
с1, с2 – векторы абсолютных скоростей при входе и выходе колеса, м/с;
α1, α2 – углы между направлениями векторов с и u;
β1, β2 – углы между направлениями векторов w и продолжением векторов u.
R1, R2 – плечо векторов с1, с2 относительно центра вращения;
r1, r2 – геометрические радиусы начала и конца лопатки рабочего колеса.
С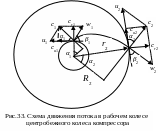
ледует
отметить, что при расчетах часто
пользуются не значениями абсолютных
скоростей, а их проекциями на направление
окружных скоростей и на радиальное
направление, так cu1
и cu2
проекции векторов абсолютных скоростей
на направления окружных скоростей и
cr1
и cк2
проекции векторов абсолютных скоростей
на радиальное (меридиональное) направление.
11.2. Уравнение теоретического давления
центробежного колеса компрессора
При рассмотрении теоретического процесса принимается, что передача мощности от вала колеса потоку газа происходит без потерь. В этом случае разность моментов количества движения представляет собой момент внешних сил, приложенных к потоку на участке межлопаточного канала на всем его протяжении от входа до выхода.
Момент количества движения представляет собой произведение транспортируемой массы текучего на скорость и на плечо, в данном случае М = ρQcR.
Теоретический момент внешних сил, приложенных к потоку на участке от входной кромки до выходной, составит
Мт =ρQт(c2R2-c1R1). (112)
Плечи R через геометрические радиусы колеса соответственно определяются, как R = r·cos α. Тогда выражение (2) представится
Мт =ρQт(c2 r2·cos α 2-c1 r1·cos α 1). (113)
Но c2·cos α 2 = сu2 и c1·cos α1 = сu1 , тогда
Мт =ρQт(cu2 r 2-cu1 r1). (114)
Подведенная к валу рабочего колеса мощность без потерь преобразуется в гидравлическую мощность потока
Nт = Мт·ω = ρQт(cu2 r 2-cu1 r1)·ω. (115)
Окружная скорость u=r·ω, тогда
Nт = Мт·ω = ρQт (cu2 u 2-cu1 u1) (116)
Nт = рт·Qт (117) Приравнивая правые части уравнений (116) и (117) , получим
рт = ρ (cu2 u 2-cu1 u1). (118)
Это уравнение было получено членом Петербургской академии наук Л. Эйлером и носит его имя.
Уравнение Эйлера (118) определяет величину полного приращения давления (теоретически полной удельной объемной работы), сообщенного лопатками колеса 1м3 текучего.