Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«Санкт-петербургский государственный университет аэрокосмического приборостроения»

РУКОВОДИТЕЛЬ

асс.				Морозов С.А.
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

Лабораторные работы на тему: Аддитивная модель

по дисциплине: Прогнозирование в условиях рынка

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР.	Z8M52K				Пирогов Д.Г.
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2013

Упражнение 1.1

За последние 11 кварталов товарооборот компании «Amada plc», скорректированный на инфляцию, составил

Год	1	2	3
Квартал	1 2 3 4	1 2 3 4	1 2 3
Товарооборот	22 28 34 27	31 43 43 41	46 53 56

Требуется:

1. В предположении существования линейного тренда построить модель с аддитивной компонентой.

2. Сделать прогноз на ближайшие три квартала. Прокомментировать вопрос о вероятной точности ваших прогнозов.

Решение:

1. Построение диаграммы временного ряда:

Товарооборот компании за последние 11 кварталов:

Дата	Номер квартала	Товарооборот
Январь - март 2009	1	22
Апрель - июнь	2	28
Июль - сентябрь	3	34
Октябрь - декабрь	4	27
Январь - март 2010	5	31
Апрель - июнь	6	43
Июль - сентябрь	7	43
Октябрь - декабрь	8	41
Январь - март 2011	9	46
Апрель - июнь	10	53
Июль - сентябрь	11	56

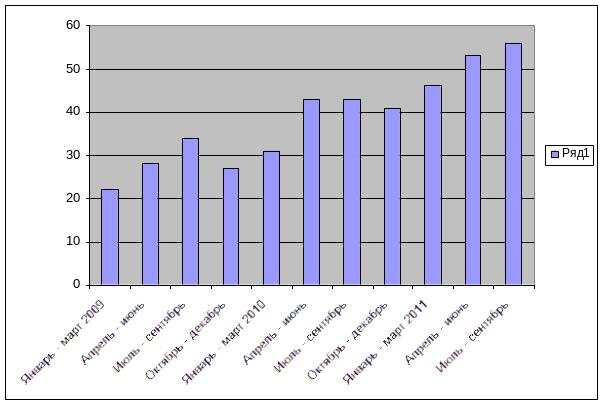
Рис1: Диаграмма временного ряда

2) Анализ модели с аддитивной компонентой: A = T + S + E

Аддитивная модель представляется как

Фактическое значение = Трендовое значение + Сезонная вариация + Ошибка,

т.е.

A = T + S + E.

2.1 Расчет сезонной компоненты методом скользящей средней (S).

Чтобы найти центрированную скользящую среднюю ищем её как среднюю двух соседних скользящих средних.

Таблица 1. Расчёт по 4 точкам центрированных скользящих средних значений тренда для модели

A - T = S + E

Дата	Объём товарооборота, тыс., A	Итого за четыре квартала	Скользящая средняя за четыре квартала	Центрированная скользящая средняя	Оценка сезонной компоненты A - T = S + E
Январь - март 2009	22
Апрель - июнь	28
		111	27,75
Июль - сентябрь	34			28,875	5,125
		120	30
Октябрь - декабрь	27			31,875	-4,875
		135	33,75
Январь - март 2010	31			34,875	-3,875
		144	36
Апрель - июнь	43			37,75	5,25
		158	39,5
Июль - сентябрь	43			41,375	1,625
		173	43,25
Октябрь - декабрь	41			44,5	-3,5
		183	45,75
Январь - март 2011	46			47,375	-1,375
		196	49
Апрель - июнь	53
Июль - сентябрь	56

Таким образом, получили десезонализированную среднюю за каждый квартал (кроме 2-х начальных и конечных).

Найдем средние значения сезонных оценок для каждого сезона года. Скорректируем средние значения, увеличивая или уменьшая их на одно и то же число (0,45) таким образом, чтобы общая их сумма была равна нулю.

Таблица 2.

Год	Номер квартала
	1	2	3	4
2009			5,125	-4,875
2010	-3,875	5,25	1,625	-3,5
2011	-1,375
Итого	-5,25	5,25	6,75	-8,375	Сумма
Оценка сезонной компоненты	-2,63	5,25	3,38	-4,19	1,81
Скорректированная сезонная компонента*	-3,1	4,8	2,9	-4,6	0

Корректируем сезонную компоненту следующим образом: полученную сумму усредненных оценок сезонных компонент делим на 4 (число кварталов) и полученное частное вычитаем из оценки сезонной компоненты, приравнивая таким образом их сумму к нулю. (Это необходимо, чтобы усреднить значения сезонной компоненты в целом за год).

Из полученных значений видно неравномерное распределение товарооборота по кварталам: положительный прирост в апреле-сентябре и отрицательный – в октябре-декабре и январе-марте.

2.2. Десезонализация данных при расчете тренда

Десезонализация заключается в вычитании соответствующих значений сезонной компоненты из фактических значений, данных за каждый квартал, т.е. A – S = T + E.

Таблица 3.

Дата	квартал	Объём товарооборота, тыс. A	Сезонная компонента S	Десезонализированный объём продаж, тыс. шт. A - S = T + E
Январь - март 2009	1	22	-3,1	25,1
Апрель - июнь	2	28	4,8	23,2
Июль - сентябрь	3	34	2,9	31,1
Октябрь - декабрь	4	27	-4,6	31,6
Январь - март 2010	5	31	-3,1	34,1
Апрель - июнь	6	43	4,8	38,2
Июль - сентябрь	7	43	2,9	40,1
Октябрь - декабрь	8	41	-4,6	45,6
Январь - март 2011	9	46	-3,1	49,1
Апрель - июнь	10	53	4,8	48,2
Июль - сентябрь	11	56	2,9	53,1
			-4,6

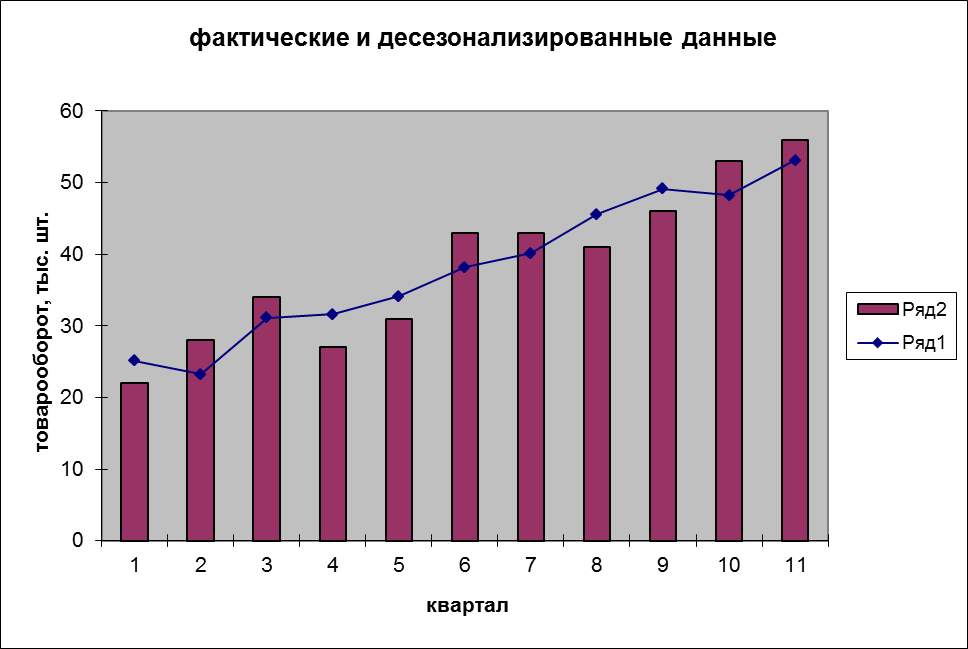
Рис.2. Фактический и десезонализирванный товарооборот.

Гистограмма с линией тренда ОХ – квартал, ОУ товарооборот. Линия тренда – оценка.

2.3. Оценка значений тренда.

T = a + b х – номер квартала, где x – порядковый номер квартала, y – значение (T + E) в предыдущей таблице. С помощью калькулятора подсчитаем:

,

,

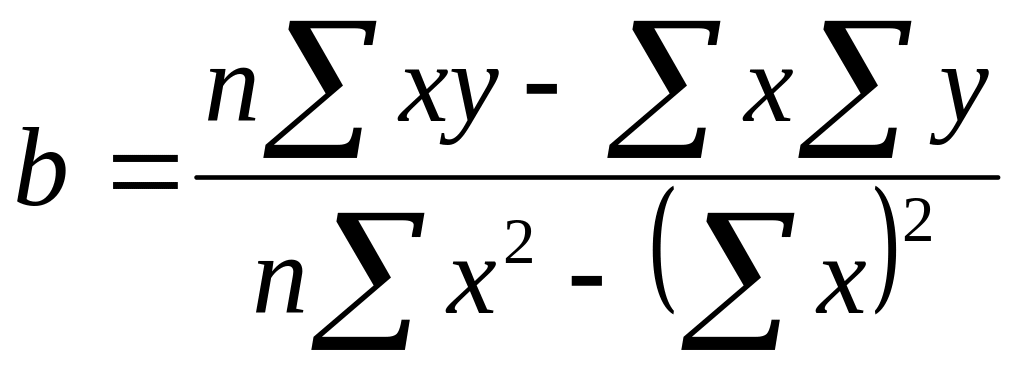 x = 66, х² =4356 ,  y =419,4

 xy =2814,25 , n =11 .

b=2,98

a=20,24

Трендовое значение объема продаж, тыс. шт: Т =20,24+2,98 x Номер квартала

2.4. Расчет ошибок или остатка.

Вычитая из фактического товарооборота значения тренда и сезонной составляющей можно найти значения ошибок.

Таблица 4.

Дата	квартал	Объём товарооборота, тыс. A	Сезонная компонента S	Трендовое значение, тыс. шт. Т	Ошибка, тыс. шт. A - S - T = E
Январь - март 2009	1	22	-3,1	23,22	1,88
Апрель – июнь	2	28	4,8	26,2	-3,00
Июль – сентябрь	3	34	2,9	29,18	1,92
Октябрь – декабрь	4	27	-4,6	32,16	-0,56
Январь - март 20010	5	31	-3,1	35,14	-1,04
Апрель – июнь	6	43	4,8	38,12	0,08
Июль – сентябрь	7	43	2,9	41,1	-1,00
Октябрь – декабрь	8	41	-4,6	44,08	1,52
Январь - март 2011	9	46	-3,1	47,06	2,04
Апрель – июнь	10	53	4,8	50,04	-1,84
Июль – сентябрь	11	56	2,9	53,02	0,08

Среднее абсолютное отклонение (MAD) или среднеквадратическая ошибка (MSE):

1,451,

2,589.

Тенденция, выявленная по фактическим данным, достаточно устойчивая и позволяет получить хорошие краткосрочные данные.

Построим графики, на котором отразим фактические данные, значения тренда и оценки