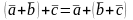Билет №8. Линейные векторные операции в геометрическом и алгебраическом видах. Векторная алгебра.

• Геометрическим вектором называется направленный отрезок прямой, который можно переносить параллельно самому себе.

• Модулем вектора называется его длина.

• Нулевым вектором называется вектор, начало и конец которого совпадают.

• Коллинеарными называются вектора, лежащие на параллельных прямых.

• Равными называются коллинеарные, со направленные вектора, имеющие одинаковую длину.

• Компланорными называются векторы, расположенные в одной и той же, или в параллельных плоскостях.

Линейные операции над векторами.

1. Сложение:

2. Умножение на число: 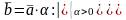Вектор, умноженный на минус единицу меняет своё направление на противоположенное.

3. Вычитание: – это сложение с вектором, умноженным на минус единицу⁴.

Теорема о взаимной колиниарности векторов.

Для всех векторов а, не равных нулю, все вектора в колиниарны а, то вектор в можно представить, как произведение вектора а на некоторое ненулевое число.

Свойства линейных операций над векторами.

1. 

2. 

3. 

4. 

Линейная зависимость и независимость геометрических векторов.

Линейной комбинацией геометрических векторов называется вектор

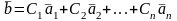
Системой из N векторов называется линейно независимой, если ни один из них не является и не может быть представлен в виде линейной комбинации других векторов этой системы.

Если линейная комбинация всех этих векторов является нулевым вектором, то в случае равенства нулю всех «С»: 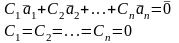, иначе если “Ci” не равно нулю, то система векторов называется линейно зависимой.

Теорема №1.

Два колиниарных вектора всегда линейно зависимы.

Теорема №2.

Три комплонарных⁵ вектора всегда линейно зависимы.

Теорема №3.

Любые четыре геометрических вектора линейно зависимы.

Базис.

Базисом на плоскости, или в пространстве называется максимальная система из линейно независимых векторов.

1. Базис на прямой является единственным вектором, параллельным данной прямой.

2. Базис на плоскости – это любая пара из не коллинеарных векторов, параллельных этой плоскости.

3. Базис в пространстве – это любые три не комплонарных вектора.

Разложение вектора по базису называется представление его в виде линейной комбинации векторов базиса.

Теорема.

Для заданного вектора а и выбранного базиса разложение, по базису является единственным.

Координаты вектора в базисе.

Координатами любого вектора в пространстве (в базисе) называются коэффициенты его разложения базису.

Свойства:

При сложении векторов одного и того же базиса, складываются соответствующие координаты.

При умножении вектора на число, умножаются все координаты этого вектора число.

Системы координат на плоскости и в пространстве:

Аффинная система координат:

Аффинной системой координат называется совокупность из точки – начала координат, и базиса.

Не аффинная система координат:

Не аффинной системой координат является полярная (цилиндрическая, сферическая) система координат.

Декартова система координат:

Частным случаем аффинной системы координат является прямоугольная Декартова система координат.

БИЛЕТ №9.

Проекция вектора на ось. Свойства проекций. Правило нахождения.

Пусть в пространстве задана некоторая прямая и единичный вектор .

Def 1. Осью будем называть прямую, по которой задано направление. Направление оси задается вектором (направляющий вектор оси).

Пусть – точка непринадлежащая . Проведем через точку плоскость ⊥ . Получим точку , которая называется проекцией (ортогональной проекцией) точки на ось . Обозначение: .

Если наряду с точкой взять точку , то можно построить .

Def 2. Так построенный вектор называется векторной проекцией вектора на ось . Обозначают: .

Иногда говорят, что есть компонента вектора на оси .

Вектора и – коллинеарны ⇒ .

Def 3. Такое число называется скалярной проекцией (проекцией) вектора на ось . Пишут: .

Таким образом .

Легко видеть, что , если ⊥ .

Свойства проекции:

Проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью:

.

Действительно, пусть .

Если (см. рис. 1), то , поэтому .

Если (см. рис. 2), то , и .

При умножении вектора на число его проекция на ось также умножается на это число:

.

Действительно, если , то λ и .

Если , то

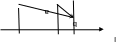
Проекция суммы векторов на ось равна сумме проекций слагаемых:

.

Действительно, это очевидно из следующих чертежей:

БИЛЕТ №10.

Скалярное произведение векторов. Свойства и приложения.

Проекция вектора на вектор.

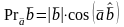
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

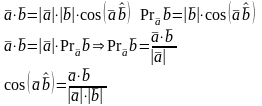
Свойства.

1. – Коммутативность.

2. 

3. 

4. 

5. 

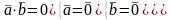
Скалярное произведение векторов, заданных своими декартовыми координатами равно сумме по парных произведений соответствующих координат сомножителей.

Применение скалярного произведения.

1. 

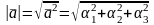
2. Определение перпендикулярности векторов, как скалярное произведение, равное нулю.

3. 

4. 

БИЛЕТ №11.

Векторное произведение векторов. Свойства и приложения.

Векторным произведением векторов называется вектор, обозначаемый 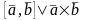, который обладает двумя свойствами:

1. Перпендикулярен двум исходным векторам.

2. Составляет с исходными векторами правую тройку⁶

3. 

Направление результирующего вектора определяется по правилу буравчика.

Свойства векторного произведения.

1. – проверка на колиниарности.

2. 

3. 

4. 

5. 

6. 

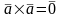
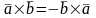
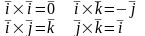
БИЛЕТ №12.

Смешанное произведение векторов. Свойства и приложения.

Смешанным произведением трёх векторов называется число, обозначаемое 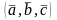, равное скалярному произведению трёх его сомножителей, на векторное произведение двух первых.

1. 0, когда , а значит угол v – острый, следовательно, вектора составляют правую тройку.

2. 0, когда , а значит угол v – тупой, следовательно, вектора составляют левую тройку.

3. 

Свойства смешанного произведения.

1. =0 тогда, когда комплонарны.

2. 

3. 

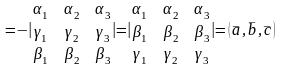
БИЛЕТ №13.

Уравнение прямой на плоскости, проходящей через заданную точку и заданным углом.

Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:

и обозначить , то полученное уравнение называется уравнением прямой с угловым коэффициентом k .

БИЛЕТ №14.

Уравнение прямой на плоскости, проходящей через заданную точку и заданным нормальным вектором.

Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.

Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).

Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно С = -1. Итого: искомое уравнение: 3х – у – 1 = 0.