Пусть теперь имеем установившееся движение жидкости, которая невязкая, несжимаемая.
И пусть она находится под воздействием сил тяжести и давления, тогда уравнение Бернулли имеет вид:
Теперь требуется идентифицировать каждое из слагаемых. Потенциальная энергия положения Z – это высота элементарной струйки над горизонтальной плоскостью сравнения. Жидкость с массой М на высоте Z от плоскости сравнения имеет некоторую потенциальную энергию MgZ. Тогда
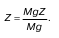
Это та же потенциальная энергия, отнесенная к единичной массе. Поэтому Z называют удельной потенциальной энергией положения.
Движущаяся частица с массой М и скоростью u имеет вес MG и кинематическую энергию U^2/2g. Если соотнести кинематическую энергию с единичной массой, то
Полученное выражение есть не что иное, как последнее, третье слагаемое в уравнении Бернулли. Следовательно, U^2/ 2 – это удельная кинетическая энергия струйки. Таким образом, общий энергетический смысл уравнения Бернулли таков: уравнение Бернулли представляет собой сумму, содержащую в себе полную удельную энергию сечения жидкости в потоке
-----
Основу теоретической части такой интерпретации составляет гидравлическое понятие напор, которое принято обозначать буквой Н, где
Гидродинамический напор Н состоит из следующих разновидностей напоров, которые входят в формулу (1) как слагаемые:
1) пьезометрический напор
2) U^2/2g – скоростной напор.
Все слагаемые имеют линейную размерность, их можно считать высотами. Назовем эти высоты:
1) z – геометрическая высота, или высота по положению;
2) p/ g – высота, соответствующая давлению p;
3) U^2/2g – скоростная высота, соответствующая скорости.
Геометрическое место концов высоты Н соответствует некоторой горизонтальной линии, которую принято называть напорной линией или линией удельной энергии.
Точно так же (по аналогии) геометрические места концов пьезометрического напора принято называть пьезометрической линией. Напорная и пьезометрическая линии расположены друг от друга на расстоянии (высоте) pатм/ g, поскольку p = pизг + pат, т. е.
Отметим, что горизонтальная плоскость, содержащая напорную линию и находящаяся над плоскостью сравнения, называется напорной плоскостью. Характеристику плоскости при разных движениях называют пьезометрическим уклоном Jп, который показывает, как изменяется на единице длины пьезометрический напор (или пьезометрическая линия):
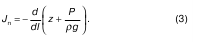
Пьезометрический уклон считается положительным, если он по течению струйки (или потока) уменьшается, отсюда и знак минус в формуле (3) перед дифференциалом. Чтобы Jп остался положительным, должно выполняться условие
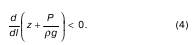
Аксиально-плунжерная гидромашина — один из видов роторно-поршневых гидромашин. У аксиально-плунжерных гидромашин диапазон регулирования частот вращения шире (500-4000 об/мин), чем урадиально-плунжерных, тогда как у большинства последних частота вращения ограничена величиной 1500 об/мин.
Данный вид гидромашин способен работать при давлениях до 40 МПа. Это несколько больше, чем у радиально-плунжерных гидромашин (до 35 МПа). Однако, есть данные, что как аксиально-плунжерные гидромашины, так и радиально-плунжерные способны работать при давлениях до 100 МПа .
Аксиально-плунжерные и аксиально-поршневые гидромашины отличаются тем, что в первых в качестве вытеснителей используются плунжеры, а во вторых — поршни. Наибольшее распространение получили аксиально-плунжерные гидромашины.
Выпускают гидромашины с наклонным диском (шайбой) и с наклонным блоком цилиндров.
Одним из достоинств аксиально-плунжерных гидромашин является возможность регулирования рабочего объёма. Изменение рабочего объёма осуществляется путём изменения угла наклона диска или угла наклона оси блока цилиндров. Максимальный угол наклона у машин с наклонным диском ограничен 15-18°. Это ограничение связано с ростом контактных нагрузок между деталями гидромашины. В то же время, в машинах с наклонным блоком рост угла наклона ограничен только конструктивными параметрами, и может достигать 40° (обычно до 25°). Но насосы с наклонным диском имеют то преимущество, что при их регулировании легко осуществляется реверс подачи (при работе в режиме насоса) или реверс направления вращения вала (при работе в режиме гидромотора); в гидромашинах с наклонным блоком реверс осуществить нельзя.
Закон вязкости (внутреннего трения) Ньютона — математическое выражение, связывающее касательное напряжение внутреннего трения (вязкость) и изменение скорости среды
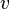в
пространстве 
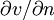(скорость
деформации) для текучих тел
(жидкостей и газов):
,
где
величина
называется
коэффициентом внутреннего трения или
динамическим коэффициентом вязкости
(единица СГС — пуаз);
с физической точки зрения она представляет
собой удельную силу трения при градиенте
скорости, равном единице. Кинематическим
коэффициентом вязкости называется
величина 
(единица СГС — Стокс,
− плотность среды).
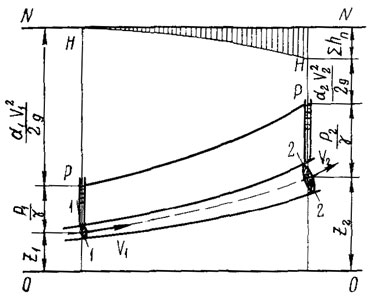На
рисунке 1 приведена диаграмма уравнения
Бернулли для потока реальной жидкости.
Здесь 0—0 —
плоскость сравнения; N—N —
плоскость начального напора; Н—Н —
напорная линия, или линия полной удельной
энергии. Падение ее на единицу длины
представляет гидравлический уклон J; Р—Р —
пьезометрическая линия, или линия
удельной потенциальной энергии. Падение
ее на единицу длины представляет
пьезометрический уклон Jп.
Так как общий запас удельной энергии вдоль потока непрерывно уменьшается, линия Н—Н всегда нисходящая, а гидравлический уклон всегда положительный (J>0). Пьезометрическая линия может быть и нисходящей, и восходящей (последнее имеет место на расширяющихся участках, когда средняя скорость потока уменьшается), поэтому пьезометрический уклон может быть и положительным (J>0), и отрицательным(J<0).
На участках с равномерным движением жидкости, где имеют место только потери напора на трение по длине, линии Н—Н и Р—Р представляют взаимно параллельные прямые, поэтому J = Jп =hдл/L. В этом случае потеря напора может быть определена по разности гидростатических напоров:
hдл = (z1 + p1/γ) - (z2 + p2/γ)