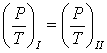1. Уравнение неразрывности - При стационарном течении количество жидкости, втекающей в единицу времени в трубку тока через сечение  , равно количеству жидкости, вытекающей через сечение   (рис. 6.1). Если поперечное сечение трубки тока бесконечно мало, то можно считать, что скорость жидкости одинакова во всех точках одного и того же поперечного сечения. Масса жидкости, протекающая за время   через поперечное сечение трубки, определяется выражением:

,

где   – плотность жидкости, а S – площадь поперечного сечения трубки. В случае стационарного течения масса   будет одной и той же для всех сечений трубки тока. Если взять два сечения, площади которых равны   и  , то можно написать:

.

Если бы это равенство не соблюдалось, то масса жидкости между сечениями   и   изменялась бы во времени. А это противоречит закону сохранения массы и предположению о стационарности течения. Если жидкость несжимаема, то  , и последнее соотношение принимает вид:

.

(6.1)

Это соотношение называется уравнением неразрывности. Его физический смысл заключается в том, что жидкость нигде не накапливается, то есть за одинаковый временной интервал в трубку тока втекает и вытекает равное количество жидкости. Скорость жидкости в одной и той же трубке тока больше там, где меньше площадь поперечного сечения трубки.

2. Гидравли́ческий уда́р (гидроудар) — скачок давления в какой-либо системе, заполненной жидкостью, вызванный крайне быстрым изменением скорости потока этой жидкости за очень малый промежуток времени. Может возникать вследствие резкого закрытия или открытия задвижки. В первом случае гидроудар называют положительным, во втором - отрицательным. Опасен положительный гидроудар. При положительном гидроударе несжимаемую жидкость следует рассматривать как сжимаемую. Гидравлический удар способен вызывать образование продольныхтрещин в трубах, что может привести к их расколу, или повреждению других элементов трубопровода. Также гидроудары чрезвычайно опасны и для другого оборудования, такого как теплообменники, насосы и сосуды, работающие под давлением. Для предотвращения гидроударов, вызванных резкой переменой направления потока рабочей среды, на трубопроводах устанавливаются обратные клапаны.

Явление гидравлического удара открыл в 1897—1899 г. Н. Е. Жуковский. Увеличение давления при гидравлическом ударе определяется в соответствии с его теорией по формуле:

,

где   — увеличение давления в Н/м²,

 — плотность жидкости в кг/м³,

 и   — средние скорости в трубопроводе до и после закрытия задвижки (запорного клапана) в м/с,

с — скорость распространения ударной волны вдоль трубопровода.

Жуковский доказал, что скорость распространения ударной волны c находится в прямо пропорциональной зависимости от сжимаемости жидкости, величины деформации стенок трубопровода, определяемой модулем упругости материала E, из которого он выполнен, а также от диаметра трубопровода.

Следовательно, гидравлический удар не может возникнуть в трубопроводе, содержащем газ, так как газ легко сжимаем.

Зависимость между скоростью ударной волны c, её длиной и временем распространения (L и   соответственно) выражается следующей формулой:

Виды гидравлических ударов

В зависимости от времени распространения ударной волны   и времени перекрытия задвижки (или другой запорной арматуры) t, в результате которого возник гидроудар, можно выделить 2 вида ударов:

Полный (прямой) гидравлический удар, если t < 

Неполный (непрямой) гидравлический удар, если t > 

3. Осевой насос — насос, в котором движение жидкости и приращение напора происходит за счет преобразования кинетической энергии.

Принцип действия

Работа осевых насосов основана на силовом взаимодействии лопасти с обтекающим ее потоком. В осевых насосах поток жидкости параллелен оси вращения лопастного колеса. Осевой насос состоит из корпуса и свободно вращающегося в нем лопастного колеса. При вращении колеса в потоке жидкости возникает разность давлений по обе стороны каждой лопасти и, следовательно, силовое взаимодействие потока с лопастным колесом. Силы давления лопастей на поток создают вынужденное вращательное и поступательное движение жидкости, увеличивая ее давление и скорость, то есть механическую энергию. Удельное приращение энергии потока жидкости в лопастном колесе зависит от сочетания скоростей протекания потока, скорости вращения колеса, его размеров и формы, то есть от сочетания конструкции, размеров, числа оборотов и подачи насоса.

4. Ламина́рное тече́ние (лат. lāmina — «пластинка») — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления).

5. Закон Пуазёйля (иногда закон Хагена — Пуазёйля) — это физический закон так называемого течения Пуазёйля, то есть установившегося течения вязкой несжимаемой жидкости в тонкой цилиндрической трубке. Закон установлен эмпирически в 1839 году Г. Хагеном, а в 1840—1841 годы — независимо Ж. Л. Пуазёйлем. Теоретически объяснён Дж. Г. Стоксом в 1845 году.

При установившемся ламинарном движении вязкой несжимаемой жидкости сквозь цилиндрическую трубу круглого сечения секундный объёмный расход прямо пропорционален перепаду давления на единицу длины трубы и четвертой степени радиуса и обратно пропорционален коэффициенту вязкости жидкости.

где

 — перепад давления на концах капилляра, Па;

 — секундный объёмный расход жидкости, м³/с;

 — радиус капилляра, м;

 — диаметр капилляра, м;

 — коэффициент динамической вязкости, Па·с;

 — длина трубы, м.

6. Параллельной работой насосов называется одновременная подача перекачиваемой жидкости несколькими насосами в общий напорный коллектор.

Насос конкретной марки работает на заданную водопроводную сеть в таком режиме, при котором энергия, сообщаемая жидкости насосом (напор насоса), равна энергии, затрачиваемой при движении жидкости по трубопроводам (требуемый напор).

Насос конкретной марки работает на заданную водопроводную сеть в таком режиме, при котором энергия, сообщаемая жидкости насосом (напор насоса), равна энергии, затрачиваемой при движении жидкости по трубопроводам (требуемый напор).

Характеристика насоса описывается уравнением  . Характеристика трубопровода может быть выражена ,где   – геометрическая высота подъема воды;   – гидравлическая характеристика трубопровода.

При работе насоса на сеть  , и совместное решение этих уравнений позволяет определить параметры   и   для конкретного случая. Графически эти параметры соответствуют точке пересечения характеристики насоса и характеристики трубопровода, называемой рабочей точкой (на рис. 1.6 это точка А).

Совместная работа насосов

 

Необходимость совместного включения насосов возникает в случаях, когда один насос не может обеспечить необходимую подачу или напор, либо необходим резерв для обеспечения бесперебойности подачи воды.

Для увеличения подачи используется параллельное соединение насосов, когда два (или более) насосов подают воду в один трубопровод. Для определения параметров работы насоса в этом случае строится совместная характеристика этих насосов. Она образуется суммированием производительности насосов при различных напорах (рис. 1.7).

 

Рис. 1.7. Параллельная работа насосов

 

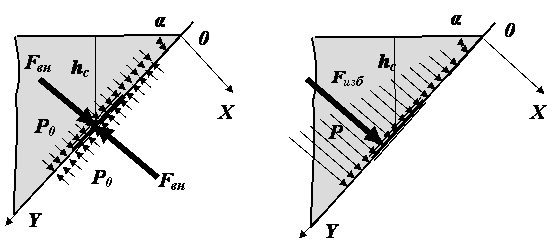
Рабочая точка в этом случае находится в точке пересечения совместной характеристики насосов и характеристики трубопровода (точка 2). При этом каждый из насосов работает с параметрами, соответствующими собственной рабочей точке (точка 1) – точками 4 и 7. Для сравнения показана рабочая точка 5и параметры работы (точки 3 и 6) при работе на эту же водопроводную сеть одного насоса. Анализ характеристик показывает, что при параллельной работе двух одинаковых насосов их подача увеличивается, но менее чем в два раза. Параллельную работу насосов целесообразно использовать при пологой характеристике трубопровода (большом диаметре и малой длине).

 

Рис. 1.8. Последовательная работа насосов

 

Для увеличения напора используется последовательное соединение насосов, когда из напорного патрубка одного насоса вода подается непосредственно во всасывающий патрубок второго насоса.

Совместная характеристика строится путем суммирования напоров насосов при одинаковых производительностях. Такая работа насосов эффективна при крутой характеристике трубопровода.

На рис. 1.8 показана последовательная работа двух одинаковых насосов на трубопровод с большим значением высоты подъема воды Н_г. При работе одного насоса (характеристика В) подача воды невозможна из-за недостаточности напора – характеристики насоса и трубопровода не пересекаются. Совместная характеристика Е пересекается с характеристикой трубопровода в рабочей точке А, которой соответствуют подача воды   и напор  .

7. hl - потери на трение по длине - пропорциональны длине потока;

hl = Kl  v^n, n=1 для ламинарного и n=2 для турбулентного движения.

Если - скоростной напор, то hl = l  v^2/2g, где l = l/d,  - коэффициент сопротивления трубы. - первая водопроводная формула

hм - местные сопротивления - потери возникают в результате изменения скорости потока на местном участке пути, в результате изменения формы и размеров поперечного сечения или направления продольной оси трубопровода; hм = м  v2/2g, где - скорость после местного сопротивления и м - коэффициент местного сопротивления. Для внезапного расширения: м = ((D/d)^2 - 1)^2, для внезапного сужения: м = (1 - (d/D)^2) / 2

В общем случае: hw = hl + hм;

8. В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т.е. напор потока Hпотока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора  ”h составят:

,

где H1-1- напор в первом сечении потока жидкости,

H2-2- напор во втором сечении потока,

h - потерянный напор - энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.

С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть

Индексами 1 и 2 обозначены характеристики потока в сечениях 1-1 и 2-2.

9. Вихревые насосы

Рабочим органом насоса является рабочее колесо с радиальными или наклонными лопатками. Колесо вращается в цилиндрическом корпусе с малыми торцовыми зазорами. Жидкость поступает через всасывающее отверстие в канал, перемещается по нему рабочим колесом и выбрасывается через выходное отверстие. Вихревой насос по сравнению с центробежным обладает следующими достоинствами: создаваемое им давление в 3-7 раз больше при одинаковых размерах и частоте вращения рабочего колеса; конструкция проще и дешевле; обладает самовсасывающей способностью; может работать на смеси жидкости и газа; подача меньше зависит от противодавления сети. Недостатками насоса являются низкий КПД, не превышающий в рабочем режиме 45%, и непригодность для подачи жидкости, содержащей абразивные частицы (так как это приводит к быстрому изнашиванию стенок торцовых и радиальных зазоров и, следовательно, падению давления и КПД). Напор вихревого насоса в 3—7 раз больше, чем центробежного, при тех же размерах и числе оборотов. Большинство вихревых насосов обладает самовсасывающей способностью, т. е. способностью при пуске засасывать жидкость без предварительного заполнения всасывающего трубопровода. Многие вихревые насосы могут работать на смеси жидкости и газа. Вихревые насосы изготовляют на подачу до 12 л/с. Напор вихревых насосов достигает 240 м, мощность доходит до 25 кВт, коэффициент быстроходности ns=6÷40. Число оборотов вихревого насоса так же, как и лопастного, ограничено только кавитационными явлениями. Следовательно, насос может быть непосредственно соединен с электродвигателем.

Рис. 1. Схема вихревого насоса 1 - рабочее колесо; 2 - лопатка; 3 - корпус; 4 - всасывающее отверстие; 5 — выходное отверстие

10. так как v = Q/, и если 8/^2*g = K, то 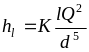- вторая водопроводная формула;

пусть K/d^5 = S, тогда 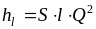- третья водопроводная формула.

11. Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение.

Прибор для измерения – вискозиметр.

Капиллярные вискозиметры

Вискозиметр с движущимся шариком

12. В водомерах Вентури расход определяется косвенным образом по разности давлений в расширенном и суженном сечениях:

Зависимость основана на уравнении Бернулли Здесь:

k — постоянное для данного водомера число;

F1 — величина площади сечения водомера при входе жидкости;

Н — разность давлений во входном и суженном сечении.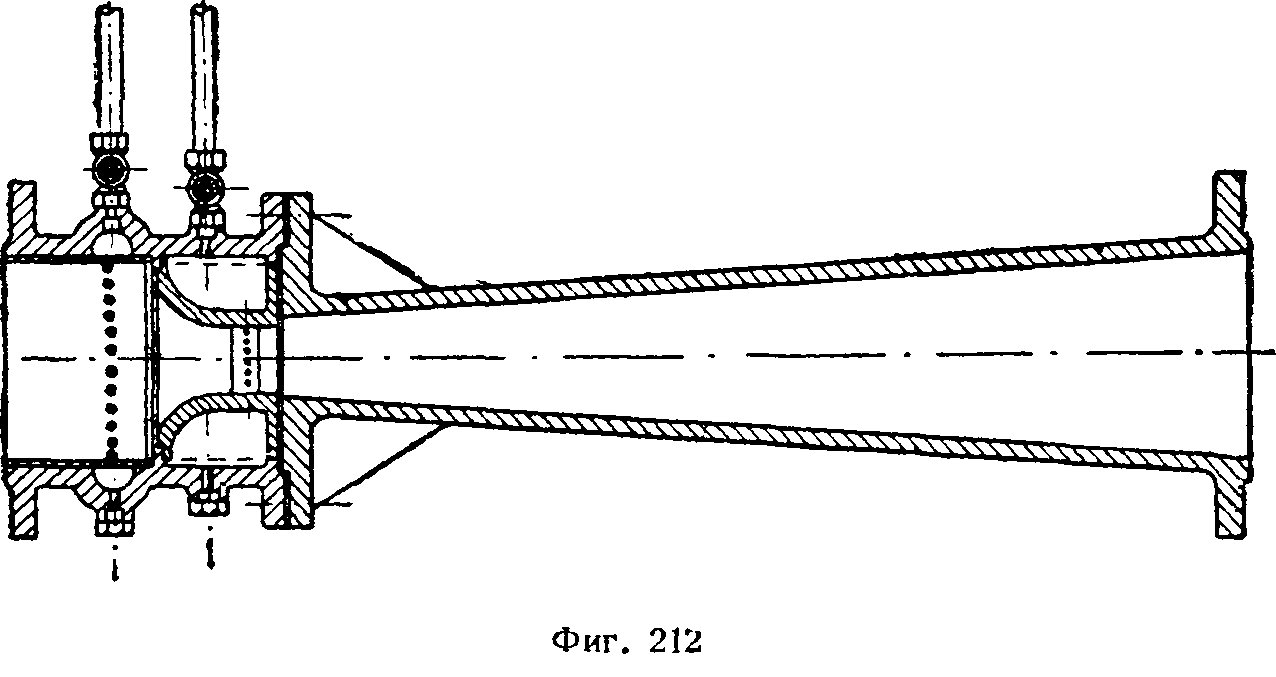

13. Давле́ние 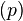  — физическая величина, численно равная силе F, действующей на единицу площади поверхности S перпендикулярно этой поверхности.

Для измерения давления используют манометры, вакуумметры, мановакуумметры

14. Пластинчатый (шиберный) самовсасывающий насос — насос предназначенный для перекачки любых в т. ч. абразивных жидких, кремо- и пастообразных труднотекучих продуктов, с кусочками и различными включениями и в т. ч. для выкачивания продуктов методом погружения всасывающего патрубка с шлангом, т. е. в отличие от некоторых так называемых самовсасывающих насосов действительно обладает способностью самовсасывания. Способен работать в обе стороны одинаково. Принцип работы насоса однократного действия состоит в следующем. При сообщении вращающего момента валу насоса ротор гидромашины приходит во вращение. Под действием центробежной силы (или под действием силы упругости пружин, находящихся под пластинами) пластины прижимаются к корпусу статора, в результате чего образуется две полости, герметично отделённых друг от друга. Объём одной из полостей постепенно увеличивается (в эту полость происходит всасывание), а одновременно с этим объём другой полости постепенно уменьшается (из этой полости осуществляется нагнетание рабочей жидкости).

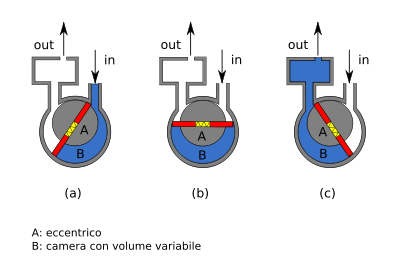
15. При ламинарном режиме движения жидкости потери напора пропорциональны средней скорости потока: hw = k_л  v,

k_л - коэффициент пропорциональности при ламинарном режиме.

16. Гидростатический напор H — это энергетическая характеристика покоящейся жидкости. Напор измеряется в метрах по высоте (вертикали). Гидростатический напор H характеризует потенциальную энергию жидкости (энергию покоя).

где z — геометрический напор или высота точки над нулевой горизонтальной плоскостью отсчёта напора ;  hp — пьезометрический напор (высота).

((((((((((((((((((((((((((

17. Гидравлическая муфта (гидромуфта, турбомуфта) — вид гидродинамической передачи, в которой, в отличие от механической муфты, отсутствует жёсткая кинематическая связь между входным и выходным валом, и, в отличие от гидротрансформатора, отсутствует реактор. Колесо, соединённое с ведущим валом, называется насосным колесом, а колесо, соединённое с ведомым валом, называется турбинным колесом.

В отличие от гидротрансформатора, моменты на насосном и турбинном колёсах всегда практически одинаковы.

Фактически насосное колесо представляет собой лопастной насос, турбинное — лопастной гидравлический двигатель. Оба эти колеса находятся в одном герметичном корпусе и максимально сближены друг с другом (но не соприкасаются), и жидкость при вращении насосного колеса попадает непосредственно на турбинное колесо, сообщая последнему вращающий момент.

Коэффициентом трансформации гидромуфты называют отношение угловой скорости ведомого вала к угловой скорости ведущего вала:

где   — угловая скорость ведомого вала;   — угловая скорость ведущего вала.

Также можно утверждать, что коэффициент трансформации равен отношению частоты вращения ведомого вала к частоте вращения ведущего вала.

Учитывая равенство моментов на ведущем и ведомом валах, можно записать, что КПД гидромуфты равен коэффициенту трансформации:

где   и   — мощность, соответственно, на ведомом и ведущем валах;   и   — момент вращения на ведомом и ведущем валах.

18. Центробежный насос — насос, в котором движение жидкости и необходимый напор создаются за счёт центробежной силы, возникающей при воздействии лопастей рабочего колеса на жидкость. Внутри корпуса насоса, который имеет, как правило, спиральную форму, на валу жестко закреплено рабочее колесо. Оно, как правило, состоит из заднего и переднего дисков, между которыми установлены лопасти. Они отогнуты от радиального направления в противоположную сторону, направления вращения рабочего колеса. С помощью патрубков корпус насоса соединяется с всасывающим и напорным трубопроводами.

Если корпус насоса полностью наполнен жидкостью из всасывающего трубопровода, то при придании вращения рабочему колесу (например, при помощи электродвигателя) жидкость, которая находится в каналах рабочего колеса (между его лопастями), под действием центробежной силы будет отбрасываться от центра колеса к периферии. Это приведёт к тому, что в центральной части колеса создастся разрежение, а на периферии повысится давление. А если повышается давление, то жидкость из насоса начнёт поступать в напорный трубопровод. Вследствие этого внутри корпуса насоса образуется разрежение, под действием которого жидкость одновременно начнёт поступать в насос из всасывающего трубопровода. Таким образом, происходит непрерывная подача жидкости центробежным насосом из всасывающего в напорный трубопровод.

Центробежные насосы бывают не только одноступенчатыми (с одним рабочим колесом), но и многоступенчатыми (с несколькими рабочими колесами). При этом принцип их действия во всех случаях остается таким же, как и всегда. Жидкость будет перемещаться под действием центробежной силы, которая развивается за счёт вращающегося рабочего колеса.

19. Распределённую нагрузку, действующую на  наклонную стенку, заменим сконцентрированной. Для этого найдём на наклонной стенке положение точки D, в которой приложена равнодействующая силы давления. Точку, в которой приложена эта сила, называют центром давления. Как уже неоднократно рассматривалось, давление, действующее в любой точке, в соответствии с основным уравнением гидростатики складывается из двух частей: внешнего давления P0, передающегося всем точкам жидкости одинаково, и давления столба жидкости P, определяемого глубиной погружения этой точки.

Давление P0 передаётся всем точкам площадки одинаково. Следовательно, равнодействующая Fвн этого давления будет приложена в центре тяжести площадки S. При этом надо учитывать, что в большинстве случаев это давление действует и со стороны жидкости и с наружной стороны стенки.

Давление P увеличивается с увеличением глубины. При этом величина равнодействующей этой силы Fизб известна и равна

,

а точку её приложения необходимо определить.

Для нахождения центра избыточного давления жидкости применим уравнение механики, согласно которому момент равнодействующей силы относительно оси 0X равен сумме моментов составляющих сил, т.е.

где YD  - координата точки приложения силы F изб,

         Y – текущая глубина.

Заменив в этом выражении Fизб и YD интегралом, в соответствии с упомянутым уравнением механики, будем иметь:

Отсюда выразим YD при этом 

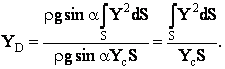
Интеграл в числителе дроби является статическим моментом инерции площади S относительно оси 0X  и обычно обозначается Jx

.

Из теоретической механики известно, что статический момент площади относительно оси вращения равен сумме собственного момента инерции (момента инерции этой площади относительно оси проходящей через её центр тяжести и параллельной первой оси) и произведению этой площади на квадрат расстояния от оси вращения до центра её тяжести

.

С учётом последнего определения YD окончательно можно выразить в виде:

.

Таким образом, разница в положениях Y (глубинах) центра тяжести площадки (т. C) и центра давления (т. D) составляет

. В итоге можно сделать следующие выводы. Если внешнее давление действует на стенку с обеих сторон, то найденная точка D будет являться центром давления.

20. Расход жидкости - объем жидкости, протекающий в единицу вре­мени через данное живое сечение потока. Расход жидкости измеряется обычно м3/с, дм3/с (или л/с), обозначается расход потока жидкости буквой Q, а расход элементарной струйки ΔQ.

Расход потока определится через расходы отдельных элементар­ных струек.

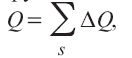
причем суммирование должно быть произведено по всему живому се­чению. Так как скорость движения u постоянная по всей площади s жи­вого сечения элементарной струйки при установившемся движении, то расход элементарной струйки оказывается равным

Применение формулы (1.46) в расчетах весьма затруднительно, так как скорости в разных струйках живого сечения потока различны. У стенок труб местные скорости меньше, а ближе к оси труб местные скорости увеличиваются. Поэтому в практических расчетах пользуют­ся понятием средней скорости потока.

Средняя скорость потока в данном сечении - воображаемая, фик­тивная скорость потока, одинаковая для всех точек данного живого се­чения, с которой через живое сечение проходил бы расход, равный фактическому.

Средняя скорость обозначается буквой V ( не следует смешивать это обозначение с обозначением местной скорости u).

Если обратиться к формуле (1.46) и заменить в ней местные ско­рости u в каждой элементарной струйке средней скоростью, то полу­чим:

21. Коэффициентом быстроходности рабочего колеса насоса называют число оборотов колеса, подобного данному, которое создает напор, равный 1 м при полезной мощности 1 л. с. в режиме максимального кпд

22. Механические приборы для измерения давления – манометры - прибор, измеряющий давление жидкости или газа.

Принцип действия манометра основан на уравновешивании измеряемого давления силой упругой деформации трубчатой пружины или более чувствительной двухпластинчатой мембраны, один конец которой запаян в держатель, а другой через тягу связан с трибко-секторным механизмом, преобразующим линейное перемещение упругого чувствительного элемента в круговое движение показывающей стрелки.

23. Гидродинамическое подобие  - это подобие потоков несжимаемой жидкости, включающее в себя подобие геометрическое, кинематическое и динамическое.

Из геометрии известно, что геометрическое подобие  означает пропорциональность сходственных размеров и равенство соответствующих угло

в. В гидравлике под геометрическим подобием понимают подобие тех поверхностей, которые ограничивают потоки жидкости, Таким образом в гидравлике геометрическое подобие означает подобие русел или трубопроводов, по которым течёт жидкость.

Кинематическое подобие это подобие линий тока и пропорциональность сходственных скоростей. Это значит, что для кинематического подобия потоков требуется соблюдение геометрического подобия.

Динамическое подобие заключается в  пропорциональности сил, действующих на сходственные элементы кинематически и геометрически подобных потоков, и равенство углов, характеризующих направление действия этих сил.

В потоках жидкостей (в нашем случае в трубопроводах, в гидромашинах и т.д.) обычно действуют разные силы – силы давления, силы вязкого трения, силы тяжести, инерционные силы. Соблюдение пропорциональности всех сил, действующих в потоке, означает полное гидродинамическое подобие.

На практике полное гидродинамическое подобие достигается редко, поэтому обычно приходится ограничиваться частичным (неполным) гидродинамическим подобием, при котором имеется пропорциональность лишь основных сил.

Записывается подобие следующим образом. Например, пропорциональность сил давления Р и сил трения Т, действующих в потоках I и II, можно записать в виде