2. Функция на участке (а, b) не является монотонной.

Имеется непрерывная случайная величина X с плотностью распре­деления f(x); другая величина Y связана с X функциональной за­висимостью:

причем функция y на участке (а, b) возможных значений аргумента не монотонна:

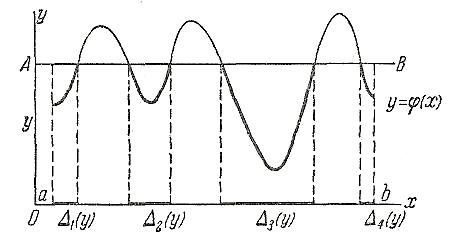
Найдем интегральную функцию распределения случайной величины Y. Для этого проведем прямую AB, параллельно оси абсцисс, на расстоянии y от нее. Выделим те участки кривой , для которых выпол­няется условие Y < у. Пусть этим участкам соответствуют участки оси абсцисс:

… .

Событие Y < у равносильно попаданию случайной величины X на один из участков

… — безразлично, на какой именно. Поэтому

Таким образом, для функции распределения величины имеем формулу:

Границы интервалов зависят от y и при заданном конкрет­ном виде функции могут быть выражены как явные функ­ции y. Дифференцируя G(y) по величине y, входящей в пределы интегралов, получим плотность распределения величины Y:

Пример. Величина X подчи­нена закону равномерной плотности на участке от до :

Найти закон распределения величины

Решение. Строим график функции :

Очевидно , , и в интервале функция немонотонна. Применяя формулу

имеем

Выразим пределы и через y:

Отсюда

Чтобы найти плотность , не будем вычислять интегралы в этой фор­муле, а непосредственно продифференцируем это выражение по пере­менной y, входящей в пределы интегралов:

Имея в виду, что , получим:

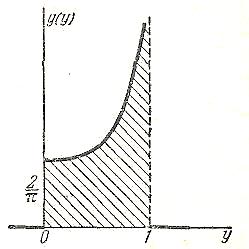
Указывая для Y закон распределения, следует оговорить, что в нашем случае он действителен лишь в пределах от 0 до 1, т.е. в тех пределах, в которых меняется при аргументе X, заключенном между и Вне этих пределов плотность g(y) равна нулю.

Ниже представлен график функции g (у). При y = 1 кривая имеет ветвь, уходящую на бесконечность.

13.3.2. Закон распределения функции двух случайных аргументов.

Определение. Если каждой паре возможных значений случайных величин X и Y соответствует одно возможное значение случайной величины Z , то Z называют функцией двух случайных аргументов X и Y:

Z =

Начнем с рассмотрения дискретных случайных величин X и Y.

Если X и Y – дискретные независимые случайные величины, то для определения закона распределения Z нужно найти все возможные значения Z и соответствующие им вероятности.

На основании полученных данных строится ряд распределения дискретной случайной величины Z.

Пример. Дискретные независимые случайные величины X и Y заданы законами распределения:

X	-2	1	3
pi	0,3	0,4	0,3

Y	0	1	2
pj	0,2	0,5	0,3

Требуется найти закон распределения дискретной случайной величины Z = X+Y.

Решение. Найдем возможные значения Z:

Сложив вероятности повторившегося дважды значения Z = 3, составим ряд распределения для Z:

Z	-2	-1	0	1	2	3	4	5
p	0,06	0,15	0,09	0,08	0,2	0,18	0,15	0,09

Перейдем к вопросу о нахождении законов распределения функций двух непрерывных случайных величин.

Постановка задачи. Имеется система двух непрерывных случайных ве­личин (X, Y) с плотностью распределения f (x, у). Слу­чайная величина Z связана с X и Y функциональной зависимостью:

Z =

Требуется найти закон распределения величины Z.

Для решения задачи вос­пользуемся геометрической интерпретацией, аналогичной той, которую мы применяли в случае одного непрерывного аргумента. Функция z = изобразится уже не кривой, а поверхностью:

Найдем интегральную функцию распределения величины Z:

Проведем плоскость Q, параллельную плоскости , на расстоя­нии от нее. Эта плоскость пересечет поверхность = по некоторой кривой К. Спроектируем кривую К на плоскость . Эта проекция, уравнение которой , разделит плоскость на две области; для одной из них высота поверхности над пло­скостью будет меньше, а для другой — больше z. Обозначим через D ту область, для которой эта высота меньше . Чтобы выполнялось неравенство , случайная точка (X, Y), очевидно, должна по­пасть в область D; следовательно,

В это выражение величина входит неявно, через пределы интегрирования.

Дифференцируя интегральную функцию распределения по , получим плотность распределения величины Z:

Зная конкретный вид функции = можно выразить пре­делы интегрирования через и написать выражение в явном виде.

Для того чтобы найти закон распределения функции двух аргу­ментов, нет необходимости каждый раз строить поверхность z = и пе­ресекать ее плоскостью, парал­лельной . На практике доста­точно построить на плоскости кривую, уравнение которой , затем выяснить, по какую сторону этой кривой Z < , а по какую Z > , и интегрировать по области D, для которой Z < .

Пример. Система случайных величин задана плотностью распределения:

Случайная величина Z зависит от X и Y так, что .

Требуется найти плотность распределения случайной величины Z.

Решение. Область интегрирования D есть пересечение области определения и области, удовлетворяющей условию или . Геометрически это означает, что область D расположена в первой четверти плоскости ниже прямой :

y

y=zx

Область D

x

0

Запишем выражение для интегральной функции распределения:

dxdy =6

Дифференцируя интегральную функцию распределения по z, получим плотность распределения случайной величины Z:

Нетрудно убедиться, что полученная функция обладает всеми свойствами плотности распределения вероятности (п.9.1.2).