12.6. Числовые характеристики системы двух случайных величин.

В п. 7 рассмотрели числовые характеристики одной дискретной случайной величины X, а в п. 10 для непрерывной. Напомним, что в качестве таких характеристик используются начальные и центральные моменты различных порядков. Из этих характеристик важнейшими являются две: математическое ожидание т_х и дисперсия D_x.

Аналогичные числовые характеристики — начальные и центральные моменты различных порядков — можно ввести и для системы двух случайных величин.

Определение. Начальным моментом порядка k, s системы (X, Y) называется

математическое ожидание произведения Х^k на Y ^s:

=

Определение. Центральным моментом порядка k, s системы (X, Y) назы­вается математическое ожидание произведения k-й и s-й степени соответствующих центрированных величин:

Эти формулы справедливы как для системы двух непрерывных случайных величин, так и для системы двух дискретных случайных величин.

На практике чаще всего находят применение начальные моменты первого порядка:

представляющие собой математические ожидания отдельно для каждой случайной величины, входящей в систему, а также центральные моменты второго порядка:

представляющие собой дисперсии отдельно для каждой случайной величины, входящей в систему.

Особую роль в качестве характеристики системы двух случайных величин, как дискретных, так и непрерывных играет второй смешанный центральный момент:

= ,

представляющий собой математическое ожидание центрированных случайных величин.

Характеристика называется корреляционным моментом или ковариацией случайных величин X и Y.

Смысл этой характеристики состоит в том, что она описывает не только степень рассеивания случайных величин X и Y, входящих в систему, но и связь между ними.

Все формулы, приведенные выше для начальных и центральных моментов относятся как к дискретным, так и к непрерывным случайным величинам.

Применительно к описанию системы двух дискретных случайных величин они принимают вид:

где суммирование распространяется на все возможные значения i, j.

Применительно к описанию системы двух непрерывных случайных величин они принимают вид:

Пример. Задан закон распределения двумерной дискретной случайной величины :

		Y
		-2	3	6
X	-0,8	0,10	0,30	0,10
	-0,5	0,15	0,25	0,10

Найти числовые характеристики системы:

Решение.

;

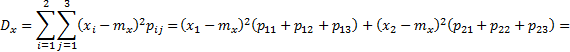
=0,025;

;

+

=

+

Выше уже говорилось, что корреляционный момент есть характеристика системы случайных величин, описывающая связь между случайными величинами, входящими в систему. Для того чтобы убедиться в этом, докажем, что для независимых случайных величин корреляционный момент равен нулю.

Доказательство проведем для непрерывных случайных величин. Пусть X, Y — независимые непрерывные величины с плотностью распределения f(х, у). В п. 12.4 мы доказали, что для независимых величин

f (x, y) = f₁ (x) f₂ (y),

где f₁ (x) f₂ (y) — плотности распределения соответственно величин X и Y.

Подставляя это выражение в формулу корреляционного момента системы непрерывных случайных величин

видим, что двойной интеграл превращается в произведение двух интегралов:

.

Интеграл представляет собой не что иное, как первый центральный момент величины X, и, следовательно, равен нулю; по той же причине равен нулю и второй сомножитель; следовательно, для независимых слу­чайных величин = 0.

Таким образом, если корреляционный момент двух случайных величин отличен от нуля, это есть признак наличия зависи­мости между ними.

Из формулы для корреляционного момента видно, что корреляционный момент характе­ризует не только зависимость величин, но и их рассеивание. Дей­ствительно, если, например, одна из величин (X, Y) весьма мало отклоняется от своего математического ожидания (почти не случайна), то корреляционный момент будет мал, какой бы тесной зависимостью ни были связаны величины (X, Y). Поэтому для характеристики связи между величинами (X, Y) в чистом виде переходят от момента к безразмерной характеристике

где — средние квадратичные отклонения величин X, Y. Эта характеристика называется коэффициентом корреляции величин X и Y. Очевидно, коэффициент корреляции обращается в нуль одновременно с корреляционным моментом; следовательно, для не­зависимых случайных величин коэффициент корреляции равен нулю.

Случайные величины, для которых корреляционный момент (а зна­чит, и коэффициент корреляции) равен нулю, называются некорре­лированными.

Выясним, эквивалентно ли понятие некоррелированности случайных величин понятию независимости. Выше мы доказали, что две независимые случайные величины всегда являются некоррелированными. Остается выяснить: справедливо ли обрат­ное положение, вытекает ли из некоррели­рованности величин их независимость? Оказывается — нет. Можно построить при­меры таких случайных величин, которые являются некоррелированными, но зави­симыми. Равенство нулю коэффициента корреляции — необходимое, но не доста­точное условие независимости случайных величин. Из независимости случайных величин вытекает их некоррелирован­ность; напротив, из некоррелированности величин еще не следует их независимость. Условие неза­висимости случайных величин — более жесткое, чем условие некор­релированности.

Убедимся в этом на примере. Рассмотрим систему случайных величин (X, Y), распределенную с равномерной плотностью внутри круга С радиуса r с центром в начале координат:

Нетрудно убедиться, что в данном примере величины являются зависимыми. Действительно, если ве­личина X приняла, например, значение 0, то величина Y может с равной вероятностью принимать все значения от -r до r; если же величина X приняла значение r, то величина Y может при­нять только одно единственное значение, в точности равное нулю. Таким образом, диапазон возможных значений Y зависит от того, какое значение приняла X.

Посмотрим, являются ли эти величины коррелированными. Вычис­лим корреляционный момент. Имея в виду, что по соображениям сим­метрии = , получим:

Для вычисления интеграла разобьем область интегрирования (круг С) на четыре сектора C₁, C₂, С₃, С₄, соответствующие четырем коор­динатным углам. В секторах C₁ и С₃ подынтегральная функция положительна, в секторах С₂ и С₄ — отрицательна; по абсолютной же величине интегралы по этим секторам равны; следовательно, инте­грал равен нулю, и величины (X, Y) не коррелированы.

Таким образом, мы видим, что из некоррелированности случай­ных величин не всегда следует их независимость.

Коэффициент корреляции характеризует не всякую зависимость, а только так называемую линейную зависимость. Линейная вероятност­ная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (или же убывать) по линейному закону. Эта тенденция к линейной зависимости может быть более или менее ярко выражен­ной, более или менее приближаться к функциональной, т. е. самой тесной линейной зависимости. Коэффициент корреляции характе­ризует степень тесноты линейной зависимости между случайными величинами. Если случайные величины X и Y связаны точной линейной функциональной зависимостью:

Y = aX+b,

то = ± 1, причем знак «плюс» или «минус» берется в зависимости от того, положителен или отрицателен коэффициент а. В общем случае, когда величины X и Y связаны произвольной вероятностной зависимостью, коэффициент корреляции может иметь значение в пре­делах: 1 < < 1.

В случае > 0 говорят о положительной корреляции вели­чин X и Y, в случае < 0 — об отрицательной корреляции.

Положительная корреляция между случайными величинами озна­чает, что при возрастании одной из них другая имеет тенденцию в среднем возрастать; отрицательная корреляция означает, что при возрастании одной из случайных величин другая имеет тенденцию в среднем убывать.

В рассмотренном выше примере двух случайных величин (X, Y), рас­пределенных внутри круга с равномерной плотностью, несмотря на наличие зависимости между X и Y, линейная зависимость отсут­ствует; при возрастании X меняется только диапазон изменения Y, а его среднее значение не меняется; естественно, вели­чины (X, Y) оказываются некоррелированными.

Если в нашем распоряжении имеются результаты ряда опытов над системой двух случайных величин (X, Y), то о наличии или отсутствии существенной корреляции между ними легко судить в первом при­ближении по графику, на котором изображены в виде точек все полученные из опыта пары значений слу­чайных величин. Например, если наблюденные пары зна­чений величин расположи­лись так, как показано на левом рисунке

то это указывает на наличие явно выражен­ной положительной корреля­ции между величинами. Еще

более ярко выраженную положительную корреляцию, близкую к ли­нейной функциональной зависимости, наблюдаем на правом рисунке.

На следующем рисунке показан случай сравнительно слабой отрицательной корре­ляции.

Наконец, проиллюстрируем случай практически некоррелированных случайных величин:

На практике, перед тем как исследовать корреляцию случайных величин, всегда полезно предвари­тельно построить наблюденные пары значений на графике для первого качественного суждения о типе корреляции.

Свойства ковариации и коэффициента корреляции

1. Если случайные величины независимы, то их ковариация, а, следовательно, и коэффициент корреляции равны нулю.

2. Область значений коэффициента корреляции:

3. Если то между случайными величинами существует линейная функциональная зависимость.

4. Ковариация случайных величин по абсолютной величине не превосходит произведение их средних квадратичных отклонений:

.

5. Корреляционный момент (ковариацию) можно вычислять по формуле