26 Деформація стиску-розтягу. Закон гука. Модуль юнга, коефіцієнт пуасона

Розтяг — один із основних видів деформацій, при якому розглядаються такі механічні характеристики, як границя пропорційності, пружності, текучості і міцності. Під терміном “розтяг–стиск” матеріалу, необхідно розуміти як дію зовнішньої сили прикладеної вздовж осі зразка і такий “розтяг-стиск” називається осьовим. Основні зміни деформаційно-осьових параметрів матеріалу визначають з діаграм розтягу-стиску в координатах  або 

Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Для тонкого растяжимого стержня закон Гука имеет вид:

Здесь   — сила, которой растягивают (сжимают) стержень,   — абсолютное удлинение (сжатие) стержня, а   — коэффициент упругости (или жёсткости).

Мо́дуль Ю́нга (модуль пружності першого роду) — характеристика пружних властивостей ізотропних речовин, один із модулів пружності.

Позначається латинською літерою E (від англ. Elasticity), вимірюється в Па, переважно в гігапаскалях. Часто його називають модулем пружності першого роду.

Модуль Юнга встановлює зв'язок між деформацією розтягу й механічним напруженням направленим на розтяг.

,

де: σ — механічне напруження, визначається, як сила, що припадає на одиницю площі поперечного перерізу тіла,

 — величина відносної деформації (відносне видовження).

Наведена формула справедлива при малих пружних деформаціях.

Коефіціє́нт Пуассо́на — це міра зміни поперечних розмірів ізотропного тіла при деформації розтягу.

Коефіцієнт Пуассона є характеристикою речовини. Він позначається грецькою літерою ν або грецькою літерою μ і є величиною безрозмірнісною.

При розтягу стержня (одновісна деформація) його поперечні розміри змінюються. Міра цієї зміни задається коефіцієнтом Пуассона за допомогою формули

,

де   — повздовжня компонента тензора деформації,   та   — поперечні компоненти тензора деформації.

27 Деформація зсуву. Кут зсуву, модуль зсуву. Закон гука

Деформація зсуву — вид деформації, при якому величина зміщення кожної точки тіла зростає в напрямку, перпендикулярному напрямку зміщення. Відносна деформація зсуву визначається за формулою:

,

Закон Гука для зсуву

Як показують експерименти у певному діапазоні деформацій, існує лінійна залежність між дотичним напруженням  , відносним зсувом   та модулем зсуву G, тобто закон Гука при зсуві:

Зв'язок трьох пружних постійних для ізотропного матеріалу (модуля Юнга E, модуля зсуву G і коефіцієнта Пуассона ν) визначається залежністю:

Отже, модуль Юнга, модуль зсуву і коефіцієнт Пуассона є характеристиками пружних властивостей матеріалу.

28 Пружні властивості реальних твердих тіл. Діаграма розтягу

Всі реальні тверді тіла під дією зовнішніх сил змінюють форму і розміри – відбувається деформація твердого тіла. При деформації відбувається зсув частинок (атомів, іонів, молекул), розташованих у вузлах кристалічної решітки, з положень рівноваги, хоча цьому і перешкоджають сили міжмолекулярної взаємодії. У разі кристалів при деформації шари кристала зрушуються один щодо одного, й при цьому відбувається рух

дислокацій.

Деформацію називають пружною, якщо після припинення дії зовнішніх сил тіло приймає первинні розміри й форму. Деформації, які зберігаються в тілі після припинення дії зовнішніх сил, називають пластичними (або залишковими). Деформації реального тіла завжди

пластичні, оскільки вони після припинення дії зовнішніх сил ніколи

повністю не зникають. Проте якщо залишкові деформації малі, то ними можна знехтувати і розглядати пружні деформації.

Не зважаючи на велику різноманітність можливих деформацій (наприклад, розтягування, стиснення, зрушення, вигин, кручення), вони можуть бути зведені до однорідних: розтягування (стиснення) і зрушення. Деформація розтягування (стиснення) характеризується відносним подовженням:

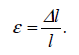
Основні зміни деформаційно-осьових параметрів матеріалу визначають з діаграм розтягу-стиску в координатах  або  (рис.1).

29 Сили тертя. Сухе тертя (ковзання, кочення) Закон Амонтона-Кулона.

Си́ла тертя́ у фізиці — це непотенційна сила, яка протидіє рухові фізичного тіла, розсіюючи його механічну енергію в тепло. Сила тертя ковзання

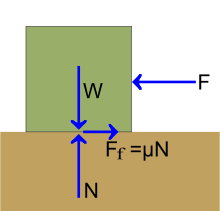
Схема дії сил при терті ковзання: W — сила ваги, N — нормальна сила реакції опори, F — прикладена сила, що заставляє тіло ковзати по поверхні, F_f — сила тертя ковзання.

Отже, як граничний випадок закону Амонтона-Кулона (див. вище), коли тіло пересувається на поверхні іншого тіла, сила тертя пропорційна силі реакції опори N з коефіцієнтом пропорційності μ, який називається коефіцієнтом тертя:

.

В техніці в залежності від умов змащування тертя ковзання поділяють на:

• сухе, коли взаємодіючі тверді тіла не розділені жодними додатковими шарами змащення. В техніці зустрічається рідко. Характерна риса сухого тертя — наявність значної сили тертя спокою;

• рідинне (в'язке), при взаємодії тіл, що розділені шаром твердого тіла (порошком графіту), рідини чи газу (мастильного матеріалу). Зустрічається в гідростатичних чи гідродинамічних опорах. Сила рідинного тертя залежить тільки від властивостей мастила та товщини його шару, а не від властивостей поверхні;

• змішане, коли область контакту містить ділянки сухого і рідинного тертя;

• граничне, коли в зоні контакту можуть міститися шари і ділянки різної природи (окисні плівки, рідина і т. д.) — напоширеніший випадок при терті ковзання.

У зв'язку зі складністю перебігу фізико-хімічних процесів, в зоні фрикційної взаємодії, процеси тертя принципово не піддаються опису методами класичної механіки.