Шифрование

Сначала исходный текст необходимо представить в двоичном виде и разбить его на блоки, равные по длине с открытым ключом. Далее из последовательности, образующей открытый ключ, выбираются только те элементы, которые по порядку соответствуют 1 в двоичной записи исходного текста, игнорируя при этом элементы, соответствующие 0биту. После этого элементы полученного подмножества складываются. Найденная в результате сумма и есть шифротекст.

Расшифровка

Расшифровка является возможной в силу того, что множитель и модуль, используемые для генерации открытого ключа из супервозрастающей последовательности, используются также и для преобразования шифротекста в сумму соответствующих элементов супервозрастающей последовательности. Далее, с помощью простого жадного алгоритма, можно расшифровать сообщение, используя O(n) арифметических операций.

13. Система Эль-Гамаля

Схема Эль-Гамаля (Elgamal) — криптосистема с открытым ключом,основанная на трудности вычисления дискретных логарифмов в конечном поле. Криптосистема включает в себя алгоритм шифрования и алгоритм цифровой подписи. Схема Эль-Гамаля лежит в основе стандартов электронной цифровой подписи в США (DSA) иРоссии (ГОСТ Р 34.10-94).

Схема была предложена Тахером Эль-Гамалем в 1984 году.^[1] Эль-Гамаль разработал один из вариантов алгоритма Диффи-Хеллмана. Он усовершенствовал систему Диффи-Хеллмана и получил два алгоритма, которые использовались для шифрования и для обеспечения аутентификации. В отличие от RSA алгоритм Эль-Гамаля не был запатентован и, поэтому, стал более дешевой альтернативой, так как не требовалась оплата взносов за лицензию. Считается, что алгоритм попадает под действие патента Диффи-Хеллмана.

Генерация ключей

1. Генерируется случайное простое число   длины   битов.

2. Выбирается случайный примитивный элемент   поля  .

3. Выбирается случайное целое число   такое, что  .

4. Вычисляется  .

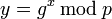5. Открытым ключом является тройка  , закрытым ключом — число  .

Работа в режиме шифрования

Шифросистема Эль-Гамаля является фактически одним из способов выработки открытых ключей Диффи — Хеллмана. Шифрование по схеме Эль-Гамаля не следует путать с алгоритмом цифровой подписи по схеме Эль-Гамаля.

Шифрование

Сообщение   шифруется следующим образом:

1. Выбирается сессионный ключ — случайное целое число   такое, что 

2. Вычисляются числа   и  .

3. Пара чисел   является шифротекстом.

Нетрудно видеть, что длина шифротекста в схеме Эль-Гамаля длиннее исходного сообщения   вдвое.

Расшифрование

Зная закрытый ключ  , исходное сообщение можно вычислить из шифротекста   по формуле:

При этом нетрудно проверить, что

и поэтому

.

Для практических вычислений больше подходит следующая формула:

Пример

• Шифрование

  1. Допустим что нужно зашифровать сообщение  .

  2. Произведем генерацию ключей :

     1. пусть 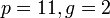 . Выберем   - случайное целое число   такое,что  .

     2. Вычислим  .

     3. Итак , открытым является тройка  ,а закрытым ключом является число  .

  3. Выбираем случайное целое число   такое, что 1 < k < (p − 1). Пусть  .

  4. Вычисляем число  .

  5. Вычисляем число  .

  6. Полученная пара   является шифротекстом.

• Расшифрование

  1. Необходимо получить сообщение   по известному шифротексту   и закрытому ключу  .

  2. Вычисляем M по формуле : 

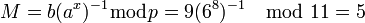
  3. Получили исходное сообщение  .

Так как в схему Эль-Гамаля вводится случайная величина  ,то шифр Эль-Гамаля можно назвать шифром многозначной замены. Из-за случайности выбора числа   такую схему еще называют схемой вероятностного шифрования. Вероятностный характер шифрования является преимуществом для схемы Эль-Гамаля, так как у схем вероятностного шифрования наблюдается большая стойкость по сравнению со схемами с определенным процессом шифрования. Недостатком схемы шифрования Эль-Гамаля является удвоение длины зашифрованного текста по сравнению с начальным текстом. Для схемы вероятностного шифрования само сообщение   и ключ не определяют шифротекст однозначно. В схеме Эль-Гамаля необходимо использовать различные значения случайной величины   для шифровки различных сообщений   и  . Если использовать одинаковые  , то для соответствующих шифротектов   и   выполняется соотношение  . Из этого выражения можно легко вычислить  , если известно  .